• Главная
• В избранное
• Наш E-MAIL
• Добавить материал
• Нашёл ошибку
• Вниз

Одна из сильных сторон PSpice заключается в способности анализировать системы с нелинейными характеристиками, например, исследовать усилитель мощности при подаче на его вход сигнала с высокой амплитудой. При этом усилитель начинает работать на нелинейной части характеристики, что приводит к искажениям в выходном напряжении. В этой главе мы выясним, насколько велики искажения, проанализировав гармонический состав выходного напряжения усилителя.

Начнем с простой схемы, позволяющей рассмотреть основные концепции, которые мы используем в дальнейшем для более сложных схем. На рис. 7.1 показано входное напряжение V_BX.p=1 В, это синусоидальная волна с частотой f=1 кГц и максимальным значением 1 В (действующим значением V_вх=√2). Чтобы обеспечить выходное напряжение, которое является нелинейной функцией входного, в качестве усилителя используется источник напряжения Е, управляемый напряжением (ИНУН). В этом примере зависимость выходного напряжения от входного отображается функцией

f(x) = 1 + х + х².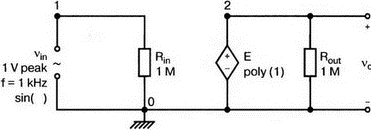

Рис. 7.1. Схема с нелинейной связью входного и выходного напряжений

Эта функциональная связь отображается в команде Е c помощью полиномиальных коэффициентов. Общий вид полинома:

f(х) = k₀ + k₁х + k₂х².

Чтобы перейти к зависимости нашего примера, используем три последних числа команды ввода Е. Мы хотим провести гармонический анализ, чтобы увидеть, какие из гармоник присутствуют в выходном напряжении, но сначала попробуем определить, чего же мы должны ожидать.

Прежде чем перейти к разложению временных зависимостей в ряд Фурье, необходимо выполнить анализ для переходных процессов (программу transient analysis в PSpice). 

Поэтому необходимо использовать обе команды .TRAN и .FOUR. Обычно выполняется анализ переходных процессов для полного периода основной частоты. В этом примере f=1 кГц; следовательно, Т=1/f=1 мс. Гармонический анализ отражает частотные компоненты вплоть до девятой гармоники. Для большинства целей этого должно быть более чем достаточно. Если показывать более высокие гармоники, они не будут иметь большого значения из-за накопления ошибки округления в результатах.

Чтобы дать более подробное описание входного напряжения V_BX, используем форму sin для описания источника. Параметры sin(а, b, с,…) означают: а — постоянная составляющая, b — максимальное значение, с — частота, d — задержка, е — коэффициент затухания и f — фаза.

При включении во входной файл команды .FOUR производится гармонический анализ, дающий разложение в ряд Фурье для результатов анализа переходного процесса. Параметры для этой команды включают частоту основной гармоники и переменные, для которых будет получено разложение. В этом примере такими переменными будут периодические функции входного V(1) и выходного V(2) напряжений. Входной файл:

Fourier Analysis; Decomposition of Polynomial

Vin 1 0 sin(0 1 1000); аргументы для смещения, максимума и частоты

Rin 1 0 1MEG

Е 2 0 poly(1) 1,0 1 1 1; последние 3 значения для k0, k1, k2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

Проведите анализ, затем получите графики V(1) и (V)2. Убедитесь, что V(1) — точная копия входного напряжения V_ВХ. Выходное напряжение должно показать компоненту постоянного тока и сложную волну с максимумом в 3 В. Из теоретического изучения рядов Фурье можно заключить, что этот график напоминает периодическую волну, состоящую из основной и второй гармоник. Целесообразно распечатать копию этого графика для будущего изучения. На рис. 7.2 показаны эти графики.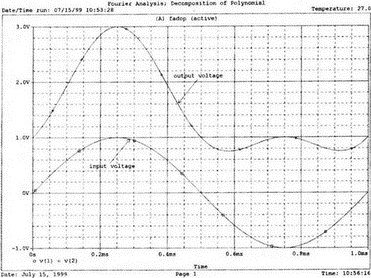

Рис. 7.2. Графики напряжений v₁ и v₂ для схемы на рис. 7.1

Рассмотрим также выходной файл для этой схемы (рис. 7.3), на котором показаны следующие значения для напряжений узлов: V(1)=0 В и V(2)=1 В. Это означает, что хотя входной сигнал не имеет смещения, выходное напряжение имеет смещение V(2)=1 В. 

На рис. 7.3 в таблице компонентов ряда Фурье для V(1) не все компоненты имеют реальные значения. Так, значение постоянной составляющей теоретически должно быть равно нулю, но анализ дает очень малое значение 3.5Е-10, не равное в точности нулю из-за накопления ошибки округления.

Fourier Analysis; Decomposition of Polynomial

Vin 1 0 sin(0 1 1000); arguments are offset, peak, and frequency

Rin 1 0 1MEG

E 2 0 poly(1) 1,0 1 1 1; last 3 1s are for k0, k1, k2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE

( 1) 0.0000  ( 2) 1.0000

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(1)

DC COMPONENT = 2.936647E-08

HARMONIC FREQUENCY FOURIER   NORMALIZED PHASE      NORMALIZED

NO       (HZ)      COMPONENT COMPONENT  (DEG)      PHASE (DEG)

1        1.000E+03 1.000E+00 1.000E+00  1.115E-06  0.000E+00

2        2.000E+03 1.994E-08 1.994E-08 -9.308E+01 -9.308E+01

3        3.000E+03 7.381E-09 7.381E-09 -9.083E+01 -9.083E+01

4        4.000E+03 4.388E-09 4.388E-09 -8.993E+01 -8.993E+01

5        5.000Е+03 3.134Е-09 3.134Е-09 -9.107Е+01 -9.107Е+01

6        6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706E+01

7        7.000E+03 1.511E-09 1.511E-09 -1.392E+02 -1.392E+02

8        8.000E+03 1.237E-09 1.237E-09 -3.990E+01 -3.990E+01

9        9.000E+03 7.642E-10 7.642E-10  3.320E+01  3.320E+01

TOTAL HARMONIC DISTORTION = 2.208405E-06 PERCENT

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(2)

DC COMPONENT = 1.500000E+00

HARMONIC FREQUENCY FOURIER   NORMALIZED PHASE      NORMALIZED

NO       (HZ)      COMPONENT COMPONENT  (DEG)      PHASE (DEG)

1        1.000E+03 1.000E+00 1.000E+00 -2.888E-07  0.000E+00

2        2.000E+03 5.000E-01 5.000Е-01 -9.000E+01 -9.000E+01

3        3.000E+03 7.971E-08 7.971E-08 -1.546E+02 -1.546E+02

4        4.000E+03 5.126Е-08 5.126Е-08 -1.439E+02 -1.439E+02

5        5.000E+03 3.918E-08 3.918E-08 -1.420E+02 -1.420E+02

6        6.000E+03 3.327E-08 3.327E-08 -1.299E+02 -1.299E+02

7        7.000Е+03 3.606E-08 3.606E-08 -1.268Е+02 -1.268E+02

8        8.000E+03 2.889E-08 2.859E-08 -1.316E+02 -1.316E+02

9        9.000E+03 2.584E-08 2.584E-08 -1.189Е+02 -1.189Е+02

TOTAL HARMONIC DISTORTION = 4.999939E+01 PERCENT

Рис. 7.3. Выходной файл с результатами анализа схемы на рис. 7.1

Первая гармоника представляет собой основную гармонику при f=1 кГц. Показана амплитуда первой гармоники ряда Фурье и ее фаза 2.4Е-7 (тоже почти ноль). Если считать, что этот компонент выражен формулой

b_nsin(nx),

то это означает, что b₁=1, n=1, где индекс 1 соответствует основной частоте. Другие гармоники могут игнорироваться, так как их амплитуды на много порядков меньше основной гармоники. Именно основная гармоника отражена на графике V(1) в Probe, получена она из данных на рис. 7.3.

Другая таблица компонентов Фурье на рис. 7.3 относится к V(2). При просмотре различных гармоник обратите внимание, что имеется постоянная составляющая в 1,5 В. Почему 1,5 В? Составляющая k₀=1 В дает только часть этого значения, остальные же 0,5 В связаны со второй гармоникой. Теория показывает, что при гармоническом искажении по второй гармонике в выходном напряжении кроме собственно второй гармоники с амплитудой b₂ появляется и связанная с искажениями по второй гармонике постоянная составляющая со значением b₀=b₂. Амплитуда основной частоты в разложении равна b₁=1 В, амплитуда второй гармоники b₂=0,5 В, ее фазовый угол составляет -90°. Более высокие гармоники имеют намного меньшую величину и их можно не учитывать.

В качестве упражнения по гармоническому синтезу вы можете нарисовать отдельные гармоники и сложить их, чтобы предсказать результат, который вы получите в Probe для V(2). Не забудьте учесть постоянную составляющую и соответствующие амплитуды и фазы для основной и второй гармоник. После того как вы нарисуете результирующее колебание, вам, несомненно, будет приятно узнать, что PSpice может сделать эту нудную работу за вас.

Создадим новый входной файл, соответствующий рис. 7.4, на котором к схеме рис. 7.1 добавлены еще два независимых источника тока. 

Мы использовали два источника только для того, чтобы вы могли получить основную и вторую гармоники на одном графике с выходным напряжением. Дополнительные источники питают подключенный параллельно 1-омный резистор. Такое изменение первоначальной схемы совсем не обязательно, просто оно оказалось удобным при данном наборе параметров. Новый входной файл представляет собой расширение предыдущего файла и выглядит следующим образом:

Fourier Analysis; Decomposition of Polynomial

Vin 1 0 sin(0 1 1000);аргументы - смещение, амплитуда и частота

Rin 1 0 1MEG

Е 2 0 poly(1) 1,0 1 1 1; последние 3 записи for k0, k1, k2

Rout 2 0 1MEG

i1 0 3 sin(1 1 1000)

i2 0 3 sin(0.5 0.5 2000 0 0 -90)

r 3 0 1

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2) V(3)

.PROBE

.END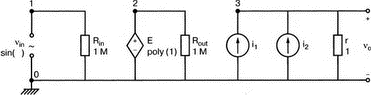

Рис. 7.4. Схема для анализа сложения гармоник и разложения в ряд Фурье 

Перед выполнением анализа подробно рассмотрим описания для i₁ и i₂. Для гармонического синтеза используются результаты разложения в ряд Фурье из предыдущей задачи. Убедитесь, что вы понимаете смысл всех параметров; затем выполните анализ в Probe, получив графики I(i1), I(i2) и I(r). Хотя они и представляют собой токи, но численно они равны напряжениям, так как проходят через сопротивление в 1 Ом. На рис. 7.5 представлены результаты. Теперь можно установить, что первый график представляет собой основную гармонику, второй — вторую гармонику, а третий — результат сложения их в резисторе r. Конечно, можно получить график V(3) вместо I(r). При этом ось Y будет размечена в единицах напряжения, а не тока. Убедитесь, что сумма двух первых кривых дает третью кривую в различные моменты времени. Чтобы сделать график более компактным, мы использовали смещение в 1 В для основной гармоники и в 0,5 В — для второй гармоники. Фактически основная гармоника имеет нулевое смещение.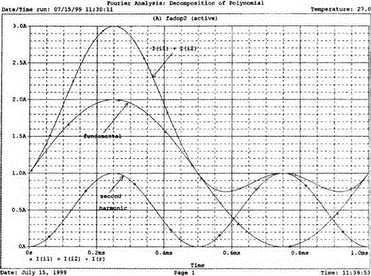

Рис. 7.5. Основная и вторая гармоники и результат их сложения

Когда рабочая область усилителя выходит за пределы линейной части характеристики, это приводит к некоторым искажениям. Первое приближение к реальной выходной кривой достигается включением в модель второй гармоники, показывающей, что переходная функция, связывающая i_c и i_b (ток коллектора и базы), является некоторой параболой. Обычно искажение намного меньше, чем принятое в нашем первом, вводном, примере, который был показан на рис. 7.1. Более точный полином задается формулой

f(x) = 0,1 + x + 0,2x².

Достаточно просто преобразовать первоначальный входной файл, чтобы он отражал эту ситуацию. Команда ввода для зависимого источника Е примет вид:

Е 2 0 poly(1) 1,0 0.1 1 0.2; последние три величины для k0, k1, k2

а весь входной файл будет:

Fourier Analysis; Second-Harmonic Distortion, Power Amplifier

Vin 1 0 sin(0 1 1000)

Rin 1 0 1MEG

E 2 0 poly(1) 1,0 0.1 1 0.2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

Проведите анализ и получите в Probe графики V(1) и V(2). Вы увидите, что обе волны выглядят, как настоящие синусоиды. Для более точного сравнения удалите график V(2) и получите вместо него график V(2)–0,1. Это позволит сблизить обе кривые. При сравнении волн не забудьте, что V(1) представляет собой просто синусоидальный сигнал, a V(2) — комбинацию основной и второй гармоник. В этом примере вторая гармоника значительно меньше по амплитуде, чем в предыдущем. Вы можете распечатать результаты исследования, приведенные на рис. 7.6.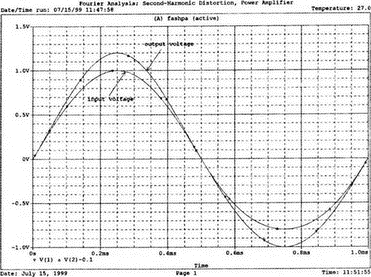

Рис. 7.6. Основная и вторая гармоники и результат их сложения

Выйдя из программы Probe, рассмотрите выходной файл для этого случая. Входное напряжение V(1) точно такое же, как и в предыдущем примере, но V(2), конечно, отличается. Обратите внимание, что постоянная составляющая выходного напряжения равна 0.2 В, а вторая гармоника при f=2 кГц имеет амплитуду 0,1 В и фазовый угол -90°. Другие гармоники намного меньше и ими можно пренебречь. В заключение определите общее гармоническое искажение, которое очень близко к 10%, как и ожидалось. Искажение по второй гармонике определено как b₁/b₂ где b₁ и b₂ — коэффициенты при второй и основной гармониках соответственно. Эти данные приведены на рис. 7.7. 

Fourier Analysis; Second-Harmonic Distortion, Power Amplifier

Vin 1 0 sin(0 1 1000)

Rin 1 0 1MEG

E 2 0 poly(1) 1.0 0.1 1 0.2

Rout 2 0 1MEG

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2)

.PROBE

.END

NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE

( 1) 0.0000  ( 2) .1000

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(1)

DC COMPONENT = 2.936647E-08

HARMONIC FREQUENCY FOURIER   NORMALIZED PHASE      NORMALIZED

NO       (HZ)      COMPONENT COMPONENT  (DEG)      PHASE (DEG)

1        1.000E+03 1.000E+00 1.000E+00  1.115E-06  0.000E+00

2        2.000E+03 1.994E-08 1.994Е-08 -9.308E+01 -9.308E+01

3        3.000E+03 7.381E-09 7.381E-09 -9.083E+01 -9.083E+01

4        4.000E+03 4.388E-09 4.388E-09 -8.993E+01 -8.993E+01

5        5.000E+03 3.134E-09 3.134Е-09 -9.107Е+01 -9.107Е+01

6        6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706Е+01

7        7.000E+03 1.511E-09 1.511E-09 -1.392E+02 -1.392E+02

8        8.000E+03 1.237E-09 1.237E-09 -3.990E+01 -3.990E+01

9        9.000E+03 7.642E-10 7.642E-10  3.320E+01  3.320E+01

TOTAL HARMONIC DISTORTION = 2.208405E-06 PERCENT

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(2)

DC COMPONENT = 2.000000E-01

HARMONIC FREQUENCY FOURIER   NORMALIZED PHASE      NORMALIZED

NO       (HZ)      COMPONENT COMPONENT  (DEG)      PHASE (DEG)

1        3.000E+03 1.000E+00 1.000E+00  7.683E-07  0.000E+00

2        2.000E+03 1.000E-01 1.000E-01 -9.000E+01 -9.000E+01

3        3.000E+03 1.756E-08 1.756E-08 -1.336E+02 -1.336E+02

4        4.000E+03 1.430E-08 1.430E-08 -1.348E+02 -1.348E+02

5        5.000E+03 9.547E-09 9.547E-09 -1.365E+02 -1.365E+02

6        6.000E+03 8.100E-09 8.100E-09 -1.232E+02 -1.232E+02

7        7.000E+03 6.463E-09 6.463E-09 -1.342E+02 -1.342E+02

8        8.000E+03 5.743E-09 5.743E-09 -9.544E+01 -9.544E+01

9        9.000E+03 6.931E-09 6.931E-09 -1.092E+02 -1.092E+02

TOTAL HARMONIC DISTORTION = 9.999880E+00 PERCENT

Рис. 7.7. Результаты анализа искажений по второй гармонике в усилителях 

Используем простую схему (рис. 7.8), чтобы показать, как две синусоидальные волны объединяются в нелинейном устройстве, использующем довольно близкие друг к другу частоты, а именно f₁=1 кГц и f₂=1,5 кГц. Нелинейное смешивание происходит в зависимом источнике е-типа VCVS (ИНУН). Полином, описывающий связь, содержит больше членов, чем в предыдущем примере:

f(x) = 1 + x + х² + x³.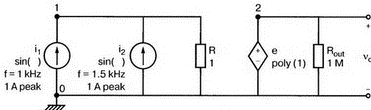

Рис. 7.8. Схема для демонстрации интермодуляционных искажений

Токи, суммируясь, создают в R=1 Ом напряжение V(1), численно равное току в R. Таким образом, входное напряжение V(1) можно воспринимать как напряжение в нелинейном смесителе. Поскольку синусоидальные волны имеют различные частоты, их сумма представляет собой сложное периодическое колебание с частотой, отличной от частоты исходных составляющих (частотой биений). Входной файл:

Intermodulation Distortion

i1 0 1 sin(0 1 1000)

i2 0 1 sin(0 1 1500)

r 1 0 1

е20 poly(1) 1,0 1 1 1 1

rout 2 0 1MEG

.tran 50us 50ms 50us

.probe

.end

Проведите моделирование и получите в Probe V(1). Выберите Plot, X-Axis Settings…, User Defined, и установите диапазон от 0 до 10 мс, чтобы достичь установившегося входного напряжения. Этот график показан на рис. 7.9. Чтобы подтвердить, что он является фактически суммой гармонических составляющих с частотами 1 и 1,5 кГц, выберем Trace, Fourier, переходя из временной в частотную область. Изменим теперь границы по оси X, установив частотный диапазон от 4 до 12 кГц. Убедитесь, что параметры осей соответствуют нужным частотам и ожидаемым амплитудам. Фактически при f=1 кГц напряжение равно 0,991 В, а при f=1,5 кГц оно составляет 0,979 В. Не забывайте, что при этом синтезе присутствует некоторая ошибка накопления. На рис. 7.10 показана соответствующая амплитудно-частотная характеристика.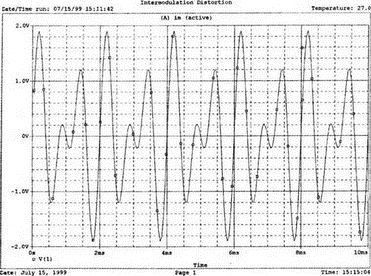

Рис. 7.9. Выходное напряжение при интермодуляционных искажениях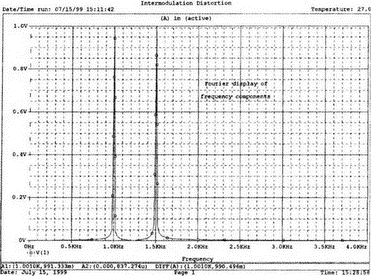 

 Рис. 7.10. Спектральный состав входного напряжения

Выберите затем Trace, End Fourier, чтобы возвратиться во временную область, удалите график V(1) и получите график напряжения на выходе смесителя V(2). Напомним, что смеситель представляет собой ИНУН с полиномиальной связью, заданной функцией f(х). Временная зависимость представляет собой график, подобный графику V(1), но при более внимательном рассмотрении можно обнаружить, что формы напряжений значительно отличаются. Кое-какие подсказки можно получить из гармонического состава этого сложного колебания, так что необходимо будет опять перейти в частотную область, выбрав диапазон по оси X от 0 до 5 кГц. Мы рекомендуем распечатать частотный спектр для дальнейшего изучения. Теоретический анализ компонентов частотной модуляции позволяет предсказывать и проверять результаты анализа на PSpice. Обратите внимание, что имеется постоянная составляющая в 2 В наряду со значительными составляющими в интервале от 0,5 до 4,5 кГц (смотри рис. 7.11 для частотного спектра).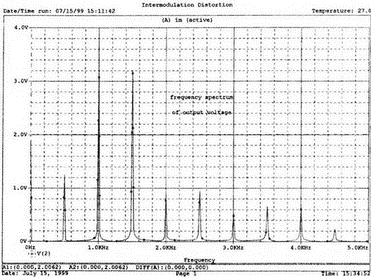

Рис. 7.11. Спектральный состав выходного напряжения 

Простейшим для теоретического анализа является случай гармонического воздействия на цепь, состоящую из линейных компонентов, таких как резисторы, конденсаторы и катушки индуктивности, и, как вы знаете, при этом реакция представляет собой гармоническое колебание с той же частотой входного сигнала. Различные падения напряжения в схеме также представляют собой гармонические колебания с той же частотой, отличающиеся только по амплитуде и фазе. Используем простую схему, чтобы проиллюстрировать некоторые из этих свойств. На рис. 7.12 показаны три источника напряжения, питающие схему, содержащую резисторы R=1 Ом и R₁=R₂=0,001 Ом. Последние два резистора требуются, чтобы сделать источники напряжения неидеальными. Используя эту схему, мы можем показать сложение синусоидальных волн в Probe. Входной файл:

Addition of Sine Waves of the Same Frequency

V1 1 0 sin (0 1 1kHz)

*Порядок следования параметров в сложном выражении для гармонических

*составляющих: смещение, амплитуда, частота, задержка, затухание, фаза

v2 2 0 sin(0 1 1kHz 0 0 45); фаза=45 градусов

v3 3 0 sin(0 1 1kHz 0 0 90); фаза=90 градусов

r1 1 2 0.001

r2 2 3 0.001

R 3 0 1

.tran 2us 2ms

.probe

.end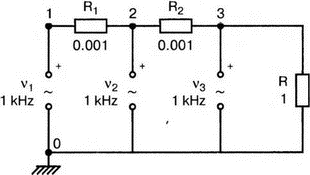

Рис. 7.12. Схема для сложения гармонических сигналов одной частоты

Выполните моделирование и в Probe получите графики v(1), v(2), и v=v(1)+v(2). Возникающие в результате графики показывают напряжение v₂ с максимумом, отстающим приблизительно на 45° от максимума v₁, и суммарное напряжение v₁+v₂ с максимумом, расположенным между их максимальными значениями. Убедитесь, что максимум v₁=1 В достигается в момент 251 мкс (90°), максимум v₂=1 В — в момент 131 мкс (47,16°) и максимум v₁+v₂=1,8381 В — в момент 171 мкс (61,56°). Удалите эти графики и получите временные зависимости для других комбинаций напряжений, например, для v(1), v(3) и v(1)+v(3). Основываясь на вашем умении складывать векторы напряжений, попытайтесь предсказать значение амплитуды для суммы напряжений до того, как получите графики в Probe, показанные на рис. 7.13.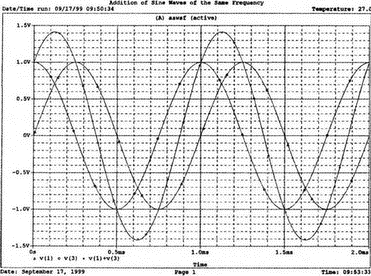

Рис. 7.13. Результат сложения гармонических сигналов одной частоты

Во входном файле, соответствующем схеме на рис. 7.12, можно легко варьировать параметры и состав источников питания. Удалим v₃ и удвоим частоту напряжения v₂, чтобы она стала частотой второй гармоники для v₁. Конечно, результирующее колебание сразу станет несинусоидальным. Фактически форма его будет зависеть от соотношения фазовых углов v₁ и v₂. Пусть в рассматриваемом примере обе гармоники достигают максимума одновременно. Входной файл для такого случая:

Adding Sine Waves; Fundamental and 2nd Harmonic Peaking Together

v1 1 0 sin(0 1 1kHz)

v2 2 0 sin(0 1 2kHz 0 0 -90)

R1 1 2 0.001

R 2 0 1

.tran 1us 1ms

.probe

.end

Проведите моделирование и получите в Probe графики v(1), v(2), и v=v(1)+v(2). Поскольку v₁ и v₂ достигают максимума одновременно, максимум результирующего колебания равен 2 В, но когда основная гармоника достигает отрицательного максимума, вторая гармоника возвращается к положительному максимуму, и их сумма обращается в нуль. Ясно, что суммарное колебание (v₁+v₂) несинусоидально. Эти графики приведены на рис. 7.14.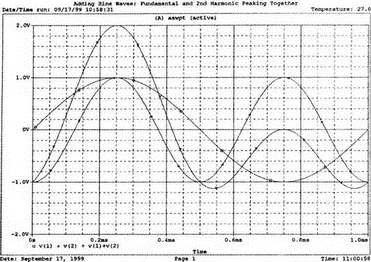

Рис. 7.14. Результат сложения первой и второй гармоник

Интересный график колебания, модулируемого по амплитуде, может быть получен в PSpice при использовании функции перемножения гармонических колебаний с существенно различными частотами. На рис. 7.15 показана схема, моделирующая такое устройство. Первым гармоническим источником является v₁ с частотой 1 кГц. Второй источник v₂ имеет частоту 20 кГц. Перемножение осуществляется в зависимом источнике е, представляющем собой ИНУН (VCVS). Резисторы необходимы, чтобы избежать появления плавающих потенциалов. Входной файл:

Multiplier for Modulated Wave

v1 1 0 sin(0 1 1000)

R1 1 0 10k

v2 2 0 sin(0 1 20000)

R2 2 0 10k

e 3 0 poly (2) 1,0 2,0 0 0 0 0 1

R3 2 0 10k

.tran 1us 1ms

.four 1000 v(1) v(2) v(3)

.probe

.end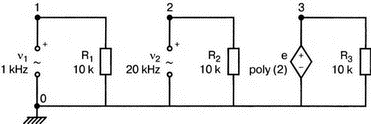

Рис. 7.15. Умножитель для модуляции синусоидального колебания

Пять последних записей в команде ввода полиномиального источника: 0 0 0 0 1. Вспомним, что это — значения коэффициентов в членах k₀, k₁v₁, k₂v₂, k₃v₁₂ и k₄v₁v₂. Все значения равны 0 за исключением k₄, который равен 1.

Проведите моделирование и получите в Probe графики v(1) и v(3). На общем графике намеренно не построена гармоническая составляющая с частотой 20 кГц, чтобы не усложнять понимание процессов. Результирующее колебание v(3) имеет классический вид амплитудно-модулированного колебания. В этом примере обе входные гармоники v₁ и v₂ имеют амплитуду 1 В. Графики приведены на рис. 7.16.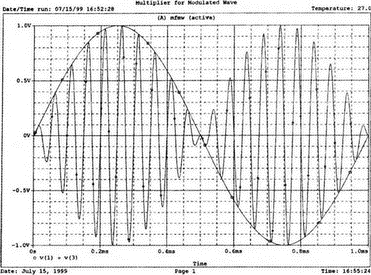

Рис. 7.16. Результат исследования амплитудно-модулированных сигналов 

Не выходя из Probe, добавьте график другого входного напряжения v(2) так, чтобы отобразить все напряжения: v(1), v(2) и v(3). Теперь этот график содержит, наряду с двумя другими волнами, и несущую, давая законченное изображение. Получите распечатку для дальнейшего изучения, затем удалите график v(2) и выберите Trace, Fourier. Установите по оси X границы диапазона от 0 до 30 кГц. В частотной области теперь отображаются составляющие с частотами 1,19 и 21 кГц. Последние компоненты представляют собой верхнюю и нижнюю побочные частоты, возникшие при такой модуляции. Определите амплитуду каждой из этих волн. Вспомните тригонометрическое тождество,

(sin a)(sin b) = 0.5[cos(a – b) – cos(a + b)],

которое объясняет амплитуды 0,5 В для частот боковой полосы. Обратитесь к рис. 7.17, на котором изображен частотный спектр. (Маркеры были удалены для получения более ясной картинки.) Проведите анализ с различными относительными амплитудами для напряжения модуляции v₁, чтобы видеть, какое влияние это оказывает на глубину модуляции т. Например, когда v₁ имеет амплитуду 0,8, что является глубиной модуляции и что напоминает результирующее колебание?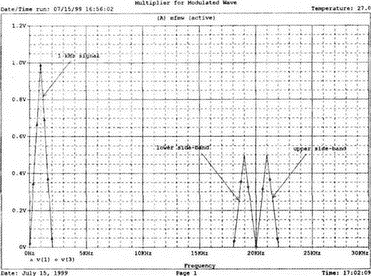

Рис. 7.17. Частотный спектр амплитудно-модулированного колебания

.FOUR<частота>*<выходные переменные>

Например, запись

.FOUR 1kHz V(1) V(2)

показывает, что выполняется разложение в ряд Фурье. Разложение может быть выполнено только после получения временной зависимости для установившегося режима, полученной при анализе переходного процесса. Такая команда должна присутствовать во входном файле: 

.TRAN <шаг><момент окончания>

Гармонический анализ дает постоянную составляющую основную гармонику, и все гармоники до девятой включительно. Показаны их амплитуды и фазы с фактическими и относительными значениями. В предшествующем примере были проанализированы V(1) и V(2) и их компоненты. Обычно для осуществления гармонического анализа используют команду .PROBE: однако вместо нее могут использоваться также команды .PRINT или .PLOT.

7.1. На рис. 7.18 полином для Е имеет форму

f(x) = х + х².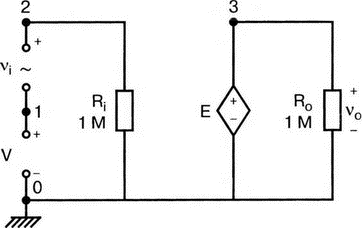

Рис. 7.18

При использовании v_i,пик=1 В, f=1 кГц и V=1 В сравните v₀ с v_i. Предскажите приблизительный гармонический состав выходного напряжения; затем выполните анализ на PSpice, который покажет гармонический состав как входного, так и выходного напряжений. В команде .FOUR используйте напряжения V(2, 1) и V(3). Исследуйте выходной файл и определите гармонический состав V(3).

7.2. В задаче 7.1, используйте Trace, Fourier, чтобы получить гармонический состав V(3). Отображая V(2,1) и V(3), установите по оси X границы от 0 до 5 кГц.

7.3. Выполните анализ для задачи 7.1 при

f(x) = 2 + 0,1x².

Предскажите приблизительный гармонический состав выходного напряжения; затем получите графики V(2,1) и V(3), чтобы проверить точность ваших предсказаний.  

7.4. На рис. 7.4 показан полиномиальный источник Е. Он был задан как

f(х) = 1 + х + х².

Замените полином на

f(х) = х + х²,

и выполните синтез и разложение, изменяя i₁ и i₂ так, чтобы ток I(r) повторял по форме напряжение V(2).

7.5. В разделе «Искажение по второй гармонике в усилителях» настоящей главы замените полином на следующий:

f(х) = 0,05 + х + 0,1х²,

и проведите анализ на PSpice так, как предложено в тексте. Получите график V(1) и (V)2–0,05, чтобы сравнить переменные составляющие входного и выходного напряжений. Предскажите значения постоянной составляющей выходного напряжения, амплитуды и фазы второй гармоники и общего гармонического искажения. Проверьте ваши предсказания, пользуясь результатами Probe и выходного файла.

7.6. В разделе «Интермодуляционные искажения» мы объединили две синусоидальные волны различных частот. Выполните анализ при частотах f₁=2 кГц и f₂=2,5 кГц, оставив выражение для f(х) без изменения. Измените команду .TRAN соответственно задаче. Выполняйте операции в том же порядке, что и в текстовом примере, чтобы проверить ваши предсказания о гармоническом составе выходного напряжения.

7.7. В разделе «Сложение гармоник» на рис. 7.12 показаны параллельные ветви с тремя источниками напряжения. Сложение гармоник было скорее математическим, чем физическим. Измените схему так, чтобы все источники напряжения были включены последовательно, затем выполните анализ снова. Получили ли вы те же результаты?

7.8. Выполните анализ, чтобы сложить следующие гармонические напряжения одной частоты f=1 кГц:

v₁ = 0,5∠0°В, v₂=1∠45°В и v₂₃=1,5∠90° В.

При этом:

а) Найдите максимальное значение (v₁+v₂), а также момент времени и фазовый угол, при котором достигается максимум.

б) Повторите пункт а) для (v₁+v₃).

При использовании режима курсора и нескольких графиков на одном экране используйте клавишу [Ctrl] и стрелки ← и →, чтобы выбрать, по какому из графиков должен двигаться курсор.

7.9. Чтобы иллюстрировать эффект сложения гармоник с близкими частотами, выполните анализ, как в задаче 7.8, для следующего набора параметров: v₁=1∠0° В, f₁=1 кГц, v₁=1∠0° В, f₂=1,2 кГц, v₁=1∠0° В и f₃=1,4 кГц:

а) Получите графики v₁, v₂ и (v₁+v₂). Найдите максимальное значение (v₁+v₂).

б) Получите графики v₁, v₃ и (v₁+v₃). Найдите максимальное значение (v₁+v₃).

7.10. Решите задачу из раздела, касающегося амплитудной модуляции, положив v₁=1 В при 1 кГц, и изменив v₁ так, чтобы глубина модуляции равнялась 0,5. Выполните анализ на PSpice, чтобы показать полученные результаты.