• Главная
• В избранное
• Наш E-MAIL
• Добавить материал
• Нашёл ошибку
• Вниз

Усилители, особенно состоящие из нескольких каскадов, могут быть устойчивы или входить в режим автоколебаний. Частота таких колебаний зависит от комбинации используемых компонентов, включая все паразитные индуктивности и емкости. Возможность возникновения колебаний появляется, когда часть выходного сигнала подается обратно на вход.

На рис. 8.1 показана блок-схема обычного контура обратной связи. Он включает суммирующее звено, в котором входной сигнал v_i складывается с сигналом обратной связи v_f. На самом деле это особый суммирующий узел, он инвертирует фазу сигнала обратной связи, что отражается знаком минус на рисунке. Разность напряжений составляет

v_d = v_i – v_f.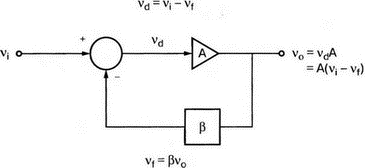

Рис. 8.1. Структурная схема усилителя с обратной связью

Напряжение v_d подается на усилитель с коэффициентом усиления по напряжению А, который создает выходное напряжение

v₀ = Av_d = A(v_i – v_f).

Выходное напряжение возвращается на суммирующее звено через цепь обратной связи, обозначенную как β. Одновременно этим символом обозначается и коэффициент передачи цепи обратной связи β=v_f/v_o, который определяет, какая часть выходного напряжения возвращается на суммирующее звено.

Предполагается, что более подробно вы можете изучить теорию, относящуюся к этому разделу, по другому учебнику. При этом учтите, что некоторые авторы могут обозначать величины, встречающиеся при изложении, другими символами.

В нашем описании коэффициент усиления в петле обратной связи задается как Аβ, то есть как произведение коэффициента усиления и коэффициента передачи в цепи обратной связи. Если принять во внимание инверсию фаз, то коэффициент усиления цепи обратной связи будет равен -Аβ. Нетрудно показать, что коэффициент усиления при замкнутой цепи обратной связи A_f равен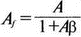

Этот коэффициент характеризует усиление при замкнутой цепи обратной связи, которое является коэффициентом усиления схемы, содержащей цепь обратной связи.

Если пришедший обратно сигнал с учетом инверсии не отличается от входного сигнала, мы можем снять входной сигнал, а сигнал на выходе усилителя будет таким же, как прежде. Это является условием возникновения колебаний, которое названо критерием Баркгаузена. На практике |Аβ| должен быть немного больше единицы. Амплитуда колебаний не будет непрерывно возрастать, как это было бы в идеальной модели, поскольку в практических случаях ее ограничивает нелинейность реальных схемных элементов.

На рис. 8.1 все напряжения могут быть заменены токами, приводя к ситуации, дуальной по отношению к предыдущей. Это означает, что входным сигналом является ток i_i, разностью — ток i_d, выходным сигналом — ток i_o=A_id, а сигнал обратной связи становится равным v_f=βi₀, обеспечивая равенство

i_d =i _i – i_f.

Коэффициент усиления в петле обратной связи по-прежнему равен Аβ или, с учетом инверсии фазы, –Аβ. Коэффициент усиления при замкнутой цепи обратной связи, как и раньше, равен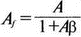

В качестве первого примера исследования генераторов рассмотрим генератор на базе моста Вина (рис. 8.2). Частота колебаний в схеме вычисляется из выражения: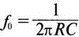

где R=R₁=R₂ и С=С₁=С₂. Примем ее равной f₀=25 кГц. Если выбрать значение С равным 1 нФ, то R=6366 Ом. Для возникновения непрерывных колебаний отношение R_f|R_g должно быть равно 2. Если выбрать R_f=20 кОм, то R_g=10 кОм. Попробуем использовать PSpice, чтобы показать, что колебания произойдут при необходимой частоте. Входной файл для такого анализа:

Wien-Bridge Oscillator

Е 2 0 4 1 2Е5

Ri 4 1 1Е6

Rg 1 0 10k

R1 3 4 6366

R2 4 0 6366

Rf 2 1 20k

C1 2 3 1nF IC=2V; начальный заряд для обеспечения колебаний

С2 4 0 1nF

.PROBE

.TRAN 0.05us 50us UIC

.END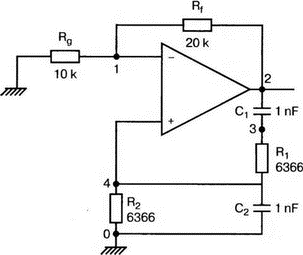

Рис. 8.2. Схема генератора на базе моста Вина

Конденсатору C₁ сообщен начальный заряд (с помощью определенного начального напряжения), чтобы создать условия, требуемые для инициирования колебаний. Если не сделать этого, анализ на PSpice покажет выходное напряжение с устойчивым нулевым значением.

Результаты, полученные в Probe, показаны на рис. 8.3. График показывает выходное напряжение v(2). Обратите внимание, что оно представляет собой гармоническое колебание с частотой f=25 кГц и амплитудой в 6 В.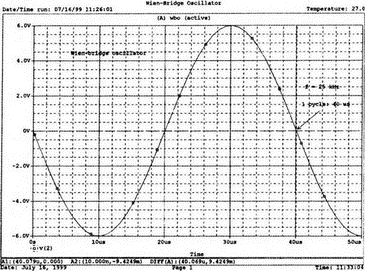

Рис. 8.3. Выходное напряжение генератора на базе моста Вина

Можно ли ожидать, что и реальный генератор даст амплитуду выходного напряжения в 6 В? Попытайтесь ответить на этот вопрос, выполнив анализ снова при начальном напряжении на конденсаторе IС=1V. Позже в этой главе мы рассмотрим также влияние на работу генератора коэффициента усиления петли обратной связи и фазового сдвига.

Генератор подстройки, использующий в цепи обратной связи два конденсатора и одну катушку индуктивности, назван генератором Колпитца. По схожей схеме построен и генератор Хартли, но в нем используются две катушки индуктивности и один конденсатор. Схема Колпитца и параметры ее компонентов показаны на рис. 8.4. Входной файл:

Colpitts Oscillator

Е 3 0 0 2 2Е5

Ri 0 2 1Е6

R1 2 1 10k

R2 2 3 20k

R 3 4 1k

C1 1 0 0.005uF

C2 4 0 0.05uF IC=2V

L 1 4 5mH

.PROBE

.TRAN 0.3us 60us UIC

.END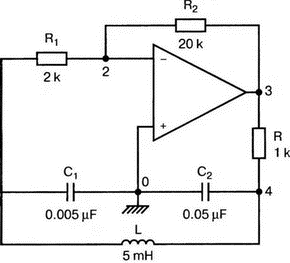

Рис. 8.4. Генератор Колпитца

Получите в Probe график выходного напряжения v(3), который показан на рис. 8.5. Убедитесь, что амплитуда возникших колебаний нарастает. Так как мы используем идеальный ОУ, в схеме не проявляется нелинейность. В практической схеме проявилось бы некоторое искажение синусоидальности колебания наряду со стабилизацией амплитуды.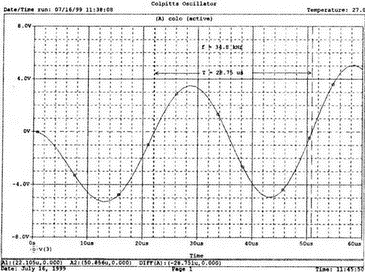

Рис. 8.5. Колебания в генераторе Колпитца

Амплитуда реального колебания определялась бы в значительной степени напряжением смещения ОУ. Обратите внимание, что частота определяется как величина, обратная периоду (разности между двумя моментами времени, в которых график напряжения пересекает ось X в одном направлении). 

На рис. 8.6 представлена схема для измерения коэффициента усиления и фазового сдвига цепи обратной связи. Схема содержит независимый источник переменного напряжения V=1 В, включенный между узлами TV₀ и TV_i (выходной и входной узел соответственно). Имеются также два ИНУН: EV_i и EV₀. Независимый источник напряжения включается в подходящее место разрыва цепи обратной связи генератора. Каждый источник зависимого напряжения нагружен на сопротивление, чтобы узлы V_i и V₀ не оказались узлами с плавающим потенциалом. Измерительная методика будет проиллюстрирована в последующих примерах.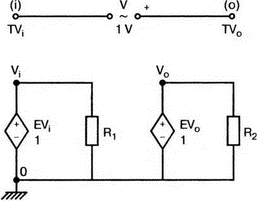

Рис. 8.6. Измерительная цепь для усилителей 

Классический RC-генератор со смещением фазы показан на рис. 8.7. Выход ОУ связан с тремя фазосмещающими RC-цепочками. Каждая цепочка производит некоторый фазовый сдвиг, и если общий сдвиг фазы, произведенный в трех цепях, равен 180°, могут происходить колебания. Кроме того, требуется выполнение условия |Aβ|=1. Анализ схемы показывает, что частота колебаний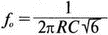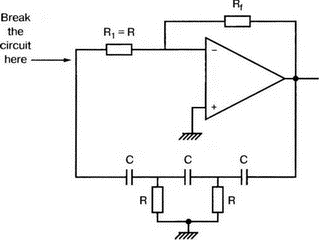

Рис. 8.7. Генератор со сдвигом фаз

Пусть, например, необходимо получить частоту колебаний f₀=100 Гц при С=0,5 мкФ и R=1,3 кОм. Анализ схемы также показывает, что при этом β=1/29; следовательно, чтобы возникли устойчивые колебания, величина |A| должна равняться 29. Практически величина |А| должна быть немного больше 29, чтобы компенсировать небольшие различия в параметрах компонентов и эксплуатационных режимах.

В схемах с инвертирующим ОУ величинам вычисляется из выражения: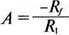

Поскольку R₁=R, это отношение преобразуется в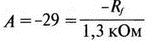

и, решая его относительно R_f, мы найдем, что R_f=37,7 кОм. Увеличив это значение на 5%, чтобы учесть ранее упомянутые отклонения, получим R_f=39,58 кОм.

Чтобы определить коэффициент усиления в петле обратной связи, воспользуемся описанной ранее схемой измерения, включив ее в разрыв, отмеченный на рис. 8.7. Таким образом, узел, соответствующий точке разрыва, превратится в два узла. Эти узлы станут узлами с плавающим потенциалом, если не показать их в подсхеме. Поэтому генератор повторно изображен на рис. 8.8, где имеется два узла разрыва: i для входа и o для выхода. Рисунок отражает также обозначения других узлов, необходимых при подготовке входного файла для PSpice. Удобно поместить ОУ в подсхему, как мы уже делали в других примерах. Упрощенная модель ОУ будет иметь такую подсхему:

.subckt iop m р vo; m инвертирующий вход, р неинвертирующий вход

rin m р 1Е6

е vo 0

р m 2Е5

.ends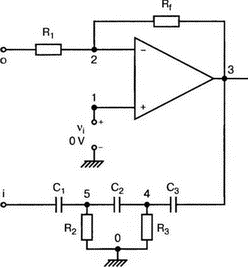

Рис. 8.8. Генератор со сдвигом фаз с разомкнутой цепью обратной связи 

Следующая часть входного файла вводит схему, показанную на рис. 8.8, показывая точки разрыва, которые позволят вставить измерительную схему. ОУ вызывается из подсхемы командой X. Эта часть входного файла:

.subckt re i о; i и о - точки разрыва схемы

х 2 1 3 iop; команда вызова ОУ

vi 1 0 1V

rf 3 2 39.58k

r1 1 2 1.3k

r2 5 0 1.3k

r3 4 0 1.3k

c1 1 5 0.5uF

c2 5 4 0.5uF

c3 4 3 0.5uF

.ends

Последняя часть входного файла показывает ссылку на подсхему генератора rc и содержит также команды, необходимые, чтобы выполнить измерения в цепи обратной связи. Эта часть содержит команды:

* loop-gain test statements

X TVi TVo re

V TVo TVi AC 1

EVi Vi 0 0 TVi 1

R1 Vi 1 1E6

EVo Vo 0 TVo 0 1

R2 Vo 0 1E6

.AC DEC 20 1Hz 10kHz

.PROBE

.END

Объединив три предшествующих фрагмента, создайте входной файл и проведите анализ. Затем получите график

20·(V(Vi)/V(Vo)).

График показывает разомкнутый коэффициент усиления цепи обратной связи. Не забудьте, что условием поддержания колебаний является |Aβ|=1. На логарифмическом графике значение соответствует не единице, а нулю. Убедитесь, что при f=100 Гц график дает почти нулевое значение (рис. 8.9).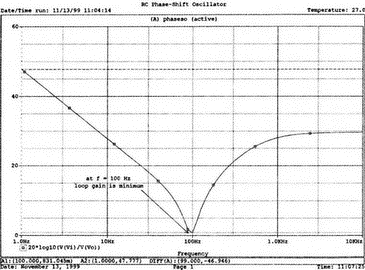

Рис. 8.9. Логарифмическая амплитудно-частотная характеристика для схемы на рис. 8.8

Теперь получите график сдвига фазы

VP(Vi) – VP(Vo),

который дает частотную зависимость разности фаз сигнала обратной связи и выходного сигнала. Убедитесь, что при f=100 Гц график показывает угол 187°. Так как анализ при разомкнутой петле обратной связи не учитывает инверсии фаз на входе, общий сдвиг фазы при замкнутой петле фактически равен 367°. Это близко к желательному углу 360°, который подразумевал бы, что усилитель не отличает входной сигнал от сигнала обратной связи, и, таким образом, колебания устойчивы. На рис. 8.10 показан график фазового сдвига.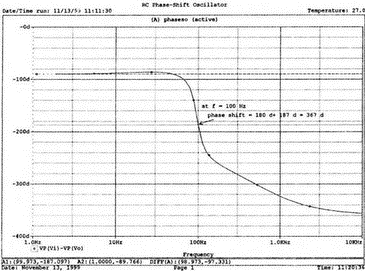

Рис. 8.10. Фазочастотная характеристика для схемы на рис. 8.8 

Другой примера генератора приведен на рис. 8.11, где показан генератор на базе моста Вина. Мост содержит последовательно включенные элементы R₁, и С₁ и параллельные элементы R₂ и С₂. Анализ этой схемы показывает, что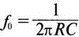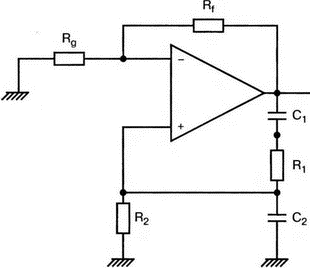

Рис. 8.11. Генератор на базе моста Вина 

Выберем f₀=25 кГц, С₁=С₂=1 нФ и R_g=10 кОм. При этом R=R₁=R₂=6366 Ом. В этой схеме необходимо обеспечить условие поддержания колебаний |Aβ|=1. Анализ также показывает, что при резонансе β= 1/3II, и необходим коэффициент усиления, равный 3. Так как коэффициент усиления неинвертирующего ОУ равен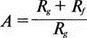

то для сопротивления обратной связи получим R_f=20 кОм.

Перерисуем теперь схему (рис. 8.11), чтобы показать параметры компонентов, разрыв для включения схемы измерения и соответствующую разметку узлов (рис. 8.12). Подсхема для генератора становится при этом частью входного файла. Весь входной файл:

Wien-Bridge Oscillator with Test Circuit

.subckt wien I i

x 2 4 1 iop

vi 1 0 0V

rg 1 2 10k

rf 2 1 20k

r1 3 4 6366

r2 4 0 6366

c1 i 3 1nF

c2 4 0 1nF

.ends

.subckt iop m p vo

rin m p 1E6

e vo 0 p m 2E5

.ends

X Tvi Tvo wien V Tvo Tvi AC 1

Evi Vi 0 0 Tvi 1

R1 Vi 0 1E6

Evo Vo 0 Tvo 0 1

R2 Vo 0 1E6

.AC DEC 40 1kHz 1MegHz

.PROBE

.END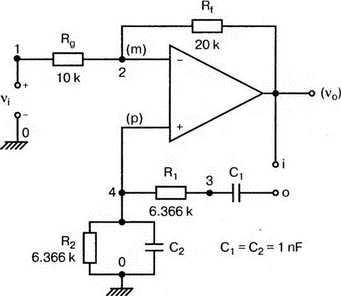

Рис. 8.12. Генератор на базе моста Вина с разомкнутой обратной связью

Проведите анализ и получите график

20·(V(Vi)/V(Vo)).

Убедитесь, что при f=25,12 кГц, коэффициент усиления достигает максимума. Он соответствует коэффициенту усиления, равному единице, так как график задан в децибелах. Затем выберем Plot и получим график сдвига фазы в цепи обратной связи:

VP(Vi) – VP(Vo),

который сообщит нам, производит ли фазосмещающая схема сдвиг фазы, необходимый для установления колебаний. Убедитесь, что при f=25,3 кГц сдвиг фазы равен -180°. Эти графики приведены на рис. 8.13.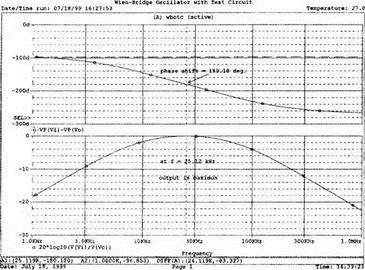

Рис. 8.13. Амплитудно-частотная и фазочастотная характеристики для схемы на рис. 8.12

Предположим теперь, что мы задали параметры элементов в схеме генератора на базе моста Вина, но не знаем частоту колебаний. Нам необходимо определить, возникнут ли колебания, и какова будет их частота. Мы рассматриваем схему той же структуры, что и в предыдущем примере, параметры элементов приведены на рис. 8.14. Входной файл:

Another Wien-Bridge Example

.subckt wien i i

vi 1a 0 0V

x 1 i 2 iop

r1 1 2 20k

r2 1 1a 20k

r3 1 0 1.5915k

r4 3 i 1.5915k

c1 2 3 0.01uF

c2 i 0 0.01uF

.ends

.subckt iop m p vo

rin m p 1E6

e vo 0 p m 2Е5

.ends

X TVi TVo wien

V TVo TVi AC 1

EVi Vi 0 0 TVi 1

R1 Vi 0 1E6

EVo Vo 0 TVo 0 1

R2 Vo 0 1E6

.AC DEC 2 0 100Hz 0.1MegHz

.PROBE

.END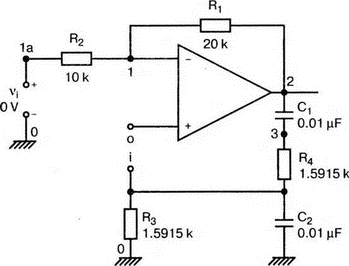

Рис. 8.14. Другая схема генератора на базе моста Вина с разомкнутой цепью обратной связи

Проведите анализ, как и в предыдущем примере, получите график

20·lg(V(Vi)/V(Vo)).

Используйте режим курсора, чтобы показать, что этот график достигает максимума при f=10 кГц. Чтобы проверить, что при этой частоте установятся колебания, получите график

VP(Vi) – VP(Vo),

и покажите, что сдвиг фазы при частоте 10 кГц равен -180°. Эти графики показаны на рис. 8.15.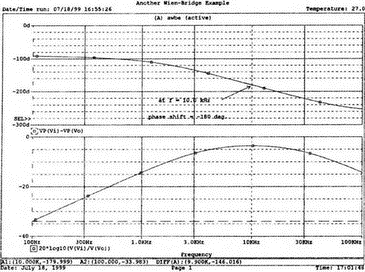

Рис. 8.15. Амплитудно-частотная и фазочастотная характеристики для схемы на рис. 8.14

Чтобы описать генератор Колпитца или генератор Хартли, зачастую используется одна и та же схема (рис. 8.16), где Z₁, Z₂ и Z₃ представляют собой полные сопротивления. Условие установления колебаний при этом задается уравнением

Z₁ + Z₂ + Z₃ = 0.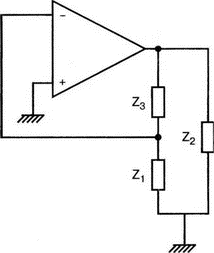

Рис. 8.16. Базовая схема для резонансных генераторов

В качестве полных сопротивлений обычно принимаются чисто реактивные сопротивления Х₁ и Х₂ одного типа и реактивное сопротивление Х₃ противоположного типа. В генераторе Колпитца сопротивления Х₁ и Х₂ емкостного характера, а Х₃ — индуктивного. Установим значения емкостей С₁=С₂=0,005 мкФ и значение индуктивности L=5 мГн.

Частота колебаний может быть найдена из уравнения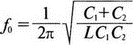

которое дает f₀=33.38 кГц. Схема для этого случая показана ранее на рис. 8.4. Параметры других компонентов: R=1 кОм, R₁=10 кОм и R₂=20 кОм.

Схема, имеющая разрыв для включения измерительной цепи, показана на рис. 8.17. Входной файл при этом приобретает вид:

Colpitts Oscillator

.subckt colpitts i i

x 2 1a 3 iop

vi 1a 0 0V

r1 i 2 10k

r2 2 3 20k

r 3 4 1k

c1 i 0 0.005uF

c2 4 0 0.05uF

L i 4 5mH

.ends

.subckt iop m p vo

rin m p 1E6

e vo 0 p m E5

.ends

X TVi TVo colpitts

V TVo TVi а.с 1

EVi Vi 0 0 TVi 1

R1 Vi 0 1E6

EVo Vo 0 TVo 0 1

R2 Vo 0 1E6

.ac DEC 1000 1kHz 100kHz

.PROBE

.END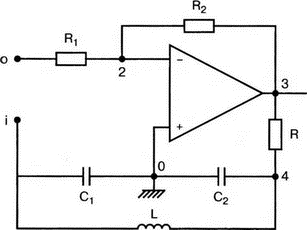

Рис. 8.17. Измерительная цепь для генератора Колпитца

Выполните анализ и получите график, подобный показанному на рис. 8.18. Обратите внимание, что имеется точка резонанса при частоте f=33,3 кГц, которая близка к предсказанной частоте колебаний. Получите график фазового сдвига между входным и выходным напряжениями и проверьте, что сдвиг фазы достигает -180° при f=33,4 кГц.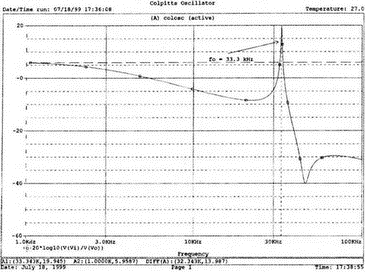

Рис. 8.18. ЛАЧХ для схемы на рис. 8.17

8.1. Генератор со сдвигом фазы, показанный на рис. 8.7, должен работать на частоте f=1 кГц. При С=1 мкФ, выберите необходимые значения компонентов и выполните анализ одним из методов, предложенных в тексте. Используя Probe, убедитесь, что схема работает в ожидаемом режиме. Распечатайте графики, полученные в программе Probe. 

8.2. Используйте генератор на базе моста Вина, показанный на рис. 8.11, настроив его на рабочую частоту f=10 кГц. Сделайте необходимые изменения в приведенном в тексте главы входном файле и выполните анализ на PSpice при задании начального заряда С₁. Используя Probe, убедитесь, что схема может поддерживать колебания при данной частоте.

8.3. Создайте схему генератора Колпитца, способного работать на частоте f=100 кГц. В качестве модели используйте схему на рис. 8.4. Применив методику разомкнутой цепи обратной связи, покажите, что колебания будут поддерживаться на этой частоте, покажите также сдвиг фазы на этой частоте.

8.4. Для генератора Колпитца из задачи 8.3 замкните контур обратной связи, и используйте необходимый метод возбуждения колебаний, чтобы показать, что колебания происходят при частоте f₀=100 кГц. Получите графики синусоидальных колебаний с помощью программы Probe.

8.5. На базе общей конфигурации LС-генератора, приведенной на рис. 8.16, разработайте генератор Хартли, где Х₁ и Х₂ — катушки индуктивности, а Х₃ — конденсатор, с такими параметрами, что f₀=50 кГц. Задайте L₁=L₂=20 мГн, считая, что между катушками индуктивности не имеется магнитной связи. Используйте PSpice/Probe, чтобы проверить правильность решения.

8.6. Схема замещения генератора со сдвигом фаз на полевом транзисторе (FET) показана на рис. 8.19. Для возникновения устойчивых колебаний |А| должен быть не меньше 29, требуя FET с μ≥29. Приняв, что g_m=5 мс, r_d=500 кОм, С=0,5 пФ, R=1,3 кОм и R_d=10 кОм, используйте метод разомкнутой обратной связи, чтобы определить, произойдут ли колебания, и если да, то на какой частоте.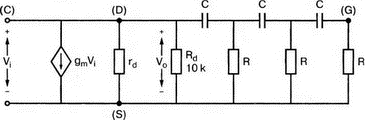

Рис. 8.19. Схема замещения генератора со сдвигом фаз на полевом транзисторе