• Главная
• В избранное
• Наш E-MAIL
• Добавить материал
• Нашёл ошибку
• Вниз

Во многих практических схемах элементы схемы ведут себя как нелинейные. Очевидна нелинейность диодов и транзисторов, которые уже использовались в многочисленных примерах этой книги. Существуют и нелинейные резисторы, например, нить лампы накаливания, нелинейные магнитные элементы типа трансформаторов на ферромагнитных магнитопроводах и им подобных. Можно ли проводить моделирование на PSpice в таких случаях? Как оказывается, это возможно.

Нелинейный резистор или другой пассивный элемент можно моделировать с помощью зависимых источников. Схема на рис. 13.1 состоит из источника напряжения и двух резисторов: R_i и R_L1. Ток через резистор R_L1 всегда является функцией приложенного к нему напряжения, но, если вы не считаете, что величина R_L1 постоянна, то эта функция не выражается законом Ома v₁=R_L1i. Если включить R_L1 в цепь обратной связи зависимого источника, то вольт-амперная характеристика полученного устройства может принимать различные формы. При использовании полиномиальной формы зависимого источника можно придать вольт-амперной характеристике любую форму, которая может быть выражена с помощью полинома. Вспомним, что выражение для полинома имеет вид

k₀ + k₁х + k₂х₂ + k₃х₃ + …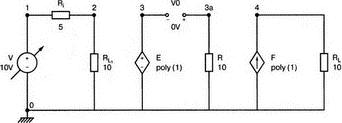

Рис. 13.1. Моделирование нелинейного резистора

Задав значения коэффициентов k, мы можем получить необходимый вид характеристики. Сделать это не всегда просто, но для некоторых случаев связь устанавливается легко. Схема на рис. 13.1 содержит два типа зависимых источников. Один из них типа Е (ИНУН) позволяет задать выходное напряжение Е с помощью напряжения v₂ на резисторе R_L1. Другой источник типа F (ИТУТ) позволяет задать выходной ток помощью тока в определенной ветви схемы. Выберем в качестве управляющего ток через резистор R.

Все команды, используемые в этом примере нам уже знакомы, и входной файл будет иметь вид: 

Variable-Resistor Simulator

VI 0 10V

Ri 1 2 5

RL1 2 0 10

E 3 0 POLY(1) 2,0 0 0.5 0.1

V0 CA 3 0V

R CA 0 10

F 0 4 POLY(1) V0 0 -0.5 0.5

RL 4 0 10

.DC V 0 14V 1V

.PROBE

.END

Выполните анализ и получите в Probe графики v(2), v(3a) и v(4). Поскольку резисторы линейны, форма токов через них будет повторять форму приложенных к ним напряжений. Обратите внимание, что только график v(2) линеен, в то время как два других имеют формы, задаваемые соответствующими полиномами. Эти графики приведены на рис. 13.2. Метод полиномиальных источников в равной степени применим и для создания таких нелинейных элементов, как конденсаторы и катушки индуктивности.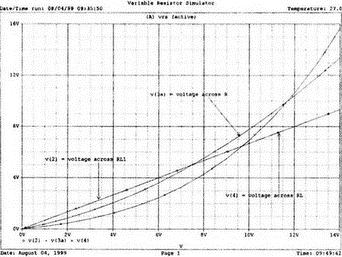

Рис. 13.2. Характеристики вход-выход для модели нелинейного резистора

В любой электрической цепи, через которую проходит ток, возбуждается также и магнитное поле. Величиной, характеризующей магнитное поле и прямо пропорциональной току I, является напряженность магнитного поля Н. Эти две величины связаны константой, которая зависит от конфигурации устройства, например для какой-либо катушки провода, от ее размера и формы. Эта связь выражается линейным уравнением Н=kI, хотя зачастую трудно найти точное значение k.

Индукция В связана с напряженностью поля уравнением В=μH. В вакууме магнитная проводимость обозначается как μ₀ и равна 4π·10^-7 Н/А2.

Когда магнитное поле распространяется в среде, отличной от вакуума, магнитную проводимость μ представляют в виде произведения μ=μ₀μ_r, где μ_r относительная магнитная проводимость среды. Последняя величина часто не является постоянной и зависит от тока.

После насыщения магнитного материала дальнейшее увеличение Н приводит лишь к незначительному увеличению В. Когда ток начинает уменьшаться, остаточная намагниченность магнитного материала изменяет зависимость В(Н), по которой индукция изменялась при увеличении тока, и в результате получается известная характеристика В(Н) с гистерезисным циклом.

PSpice использует для описания ферромагнитной катушки индуктивности — модели, основанной на теории Джилеса-Атертона (Jiles-Atherton) для магнитных доменов (ссылка в соответствующем разделе приложения E). Полное описание этой модели выходит за рамки данной работы, однако мы можем исследовать кривую В(Н) для различных условий и посмотреть, что происходит с токами и напряжениями в трансформаторах при насыщении.

Схема на рис. 13.3 содержит ферромагнитную катушку с обмоткой в 20 витков и сопротивлением R_L=10 Ом. Обратите внимание, что команда для катушки индуктивности выглядит как

L1 1 0 20

где 20 представляет именно количество витков, а не индуктивность в 20 Гн. Это связано с присутствием во входном файле команды для модели, содержащей ключевое слово core. Если не использовать модель, последний параметр будет означать 20 Гн. Четыре генератора тока используются для создания низкочастотных синусоидальных колебаний с частотой 1 Гц. Первый генератор создает ток с максимальным значением 0,1 А и началом в момент t=0.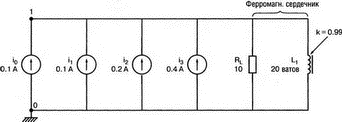

Рис. 13.3. Цепь для моделирования процесса в стальном магнитопроводе

Затем при t=1 с подключается следующий источник тока. Он также имеет максимальное значение 0,1 А. Затем подключаются третий и четвертый источники синусоидального тока в начале второй и третьей секунды соответственно. Амплитуда синусоидального тока увеличивается, чтобы показать влияние насыщения. Команда .MODEL использует ключевое слово core и позволяет учесть нелинейные магнитные параметры модели магнитопровода. Входной файл при этом: 

This is the sample magnetic core problem

I0 0 1 sin(0 0.1A 1Hz 0)

I1 0 1 sin(0 0.1A 1Hz 1)

I2 0 1 sin (0 0.2A 1Hz 2)

I3 0 1 sin(0 0.4A 1Hz 3) RL 1 0 10

L1 1 0 20; - число витков =20, а не L = 20 Гн (используется модель)

K1 LI 0.99 KT; коэффициент связи

.model KT Core(MS=420E3 А=26 K=18 С=1.05 AREA=1.17 РАТН=8.49)

.options ITL5=0

.tran 0.1 4

.probe

.end

Выполните анализ в Probe и получите график В(K₁) в функции времени. Он показывает нелинейную индукцию в магнитопроводе на временном интервале от 0 до 4 с. Обратите внимание, что на первых периодах нелинейность невелика по сравнению с более поздними периодами. Убедитесь, что значение первого максимума составляет В=1864 Э (эрстед), второй достигается при В=2965 Э, третий — при В=3989 Э, и заключительный — при B=4593 Э. Временная диаграмма приведена на рис. 13.4.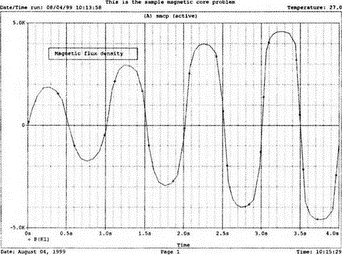

Рис. 13.4. Временная диаграмма магнитной индукции в магнитопроводе

Чтобы получить стандартную петлю гистерезиса В(Н), замените величину, отложенную по оси Х на H(R₁). Она представляет собой напряженность магнитного поля в магнитопроводе, пропорциональную току. По оси Y по-прежнему откладывается величина B(R_i). На рис. 13.5 представлен этот график. Четыре петли гистерезиса соответствуют четырем уровням тока. Посмотрите, где на этой кривой появляются максимальные значения, показанные на предыдущем графике. Попробуйте изменить число витков, выполнить анализ снова и сравнить полученные результаты с предыдущими.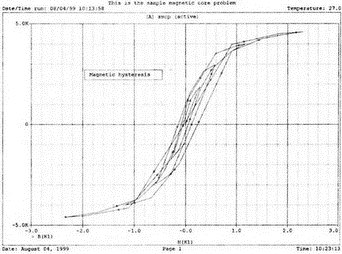

Рис. 13.5. Магнитный гистерезис в стальном магнитопроводе

Когда используется трансформатор с магнитопроводом из электротехнической стали, нелинейность характеристики магнитопровода влияет на форму тока вторичной обмотки. Чтобы показать это, рассмотрим схему (рис. 13.6), на которой представлен трансформатор, к первичной обмотке которого подключен источник тока. Параллельно источнику тока подключен резистор R₁, поскольку трансформатор нельзя подключать к идеальному источнику тока.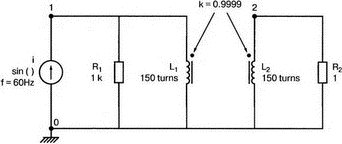

Рис. 13.6. Схема замещения трансформатора со стальным магнитопроводом

Первичная и вторичная обмотки содержат по 150 витков. Входной файл:

Iron-Core Transformer

i 0 1 sin (0 1А 60Hz)

R1 1 0 1k

L1 1 0 150 ; число витков первичной обмотки = 150

L2 2 0 150 ; число витков вторичной обмотки = 150

R2 2 0 1

K1 L1 L2 0.9999 KT

.model KT core ;- используется модель магнитопровода по умолчанию

.options ITL5 = 0

.tran 1ms 16.67ms

.end

Проведите анализ и получите в Probe графики i(R2) и i(L1). Убедитесь в том, что хотя первичный ток имеет форму синусоиды, вторичный ток сильно искажен. Эти графики приведены на рис. 13.7.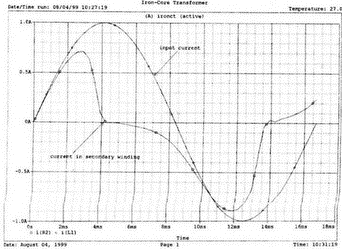

Рис. 13.7. Искажения формы тока вторичной обмотки трансформатора при сильном насыщении магнитопровода

Измените значение R₂ и/или число витков каждой обмотки и сравните результаты с полученными ранее. Чтобы показать, что получается при меньшей степени насыщения, используйте следующий входной файл:

Iron-Core Transformer with Less Saturation

I 0 1 sin (0 1A 60Hz)

R1 1 0 1k

L1 1 0 10; 10 витков первичной обмотки

L2 2 0 150; 150 витков вторичной обмотки

R2 2 0 1

K1 L1 L2 0.9999 KT

.model KT core

.options ITL5 = 0

.tran 1ms 16.67ms

.probe

.end

Выполните анализ и получите в Probe графики i(R₂) и i(L₁)/20. Последний график масштабирован, чтобы облегчить сравнение двух кривых. Из рис. 13.8, где представлен результат моделирования, можно видеть, что обе кривые — почти синусоидальны. Однако вторичный ток по-прежнему несколько искажен.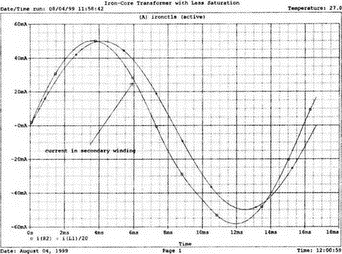

Рис. 13.8. Искажения формы тока вторичной обмотки трансформатора при допустимом насыщении магнитопровода

Вы можете попробовать несколько других сочетаний сопротивления и числа витков, чтобы лучше понять, как работает основная модель. Вы обнаружите, что для некоторых сочетаний процесс моделирования в PSpice не сходится. 

Другой способ получения нелинейного резистора состоит в использовании ключа, управляемого напряжением или током. Такой ключ может размыкаться или замыкаться в зависимости от значения напряжения или тока в другой части схемы. 

На рис. 13.9 представлен ключ, управляемый напряжением, включенный последовательно с источником напряжения V=10 В и резисторами R_i=50 Ом и R_l=50 Ом. Если выбрать напряжение V в качестве управляющего, то ключ может замыкаться при достижении напряжением заданного значения.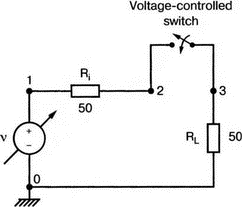

Рис. 13.9. Модель нелинейного сопротивления с ключом, управляемым напряжением

Ключ в замкнутом состоянии имеет номинальное значение сопротивления RON=1 Ом, а в разомкнутом состоянии ROFF=1 МОм. Сопротивление в разомкнутом состоянии вводится, чтобы предотвратить появление узла с плавающим потенциалом. Модель вводится с помощью команды, включающей имя vswitch и описание режима переключения. Чтобы определить условия, при которых ключ находится в замкнутом и разомкнутом состояниях, выберите напряжение включения VON=3 В и используйте для напряжения выключения VOFF, значение, заданное по умолчанию VOFF=0. Входной файл:

Voltage-Controlled Switch

v 1 0 10V

Ri 1 2 50

RL 3 0 5 0

S 2 3 1 0 S1; имя ключа, управляемого напряжением, должно начинаться с S

.model SI vswitch(RON=1 ROPF=1E6 VON=3V VOPF=0)

.dc v 0 10V 0.05V

.probe

.end

Проведите анализ и получите график i(R_i). Обратите внимание, что кривая показывает почти нулевое значение тока, пока входное напряжение не приближается к значению 2 В. Затем к моменту, когда входное напряжение достигает VON=3 В, наклон кривой отражает сопротивление контура при замкнутом ключе. В состав этого сопротивления, равного 101 Ом, входит и сопротивление самого ключа. Этот график приведен на рис. 13.10.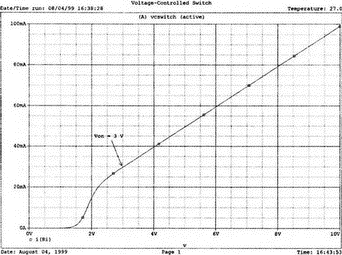

Рис. 13.10. ВАХ модели нелинейного резистора, представленной на рис. 13.9

Измените значение VON на 8 В и снова проведите анализ. Вы должны получить график, подобный показанному на рис. 13.11. Наблюдайте изменения в начале вольт-амперной характеристики. Ток начинает повышаться вблизи 4 В. Не забудьте, что наклон кривой обратно пропорционален сопротивлению контура. Обратите внимание, что наклон кривой изменяется плавно; не наблюдается никакого резкого изменения при значении VON. Вы должны учитывать это при использовании такого ключа в схемах. Перед использованием управляемого напряжением ключа в сложной схеме желательно получить ВАХ, подобную приведенной здесь.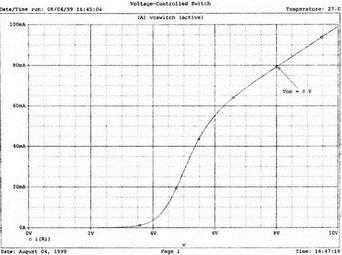

Рис. 13.11. ВАХ модели нелинейного резистора при напряжении переключения в 8 В

Как вариант, дуальный ключу, управляемому напряжением, может использоваться ключ, управляемый током. В этом случае включение ключа происходит при определенном значении тока в какой-либо ветви схемы. На рис. 13.12 приведена схема, в которой имеется источник тока, подключенный к двум ветвям, каждая из которых содержит резистор сопротивлением 100 Ом. Правая ветвь содержит, кроме того, ключ W. Пока ключ не замкнут, сопротивление этой ветви очень высоко ROFF=1 МОм. Когда ток в левой ветви достигает установленного значения (тока включения) ION=10 мА, ключ в правой ветви замыкается. Значение ION по умолчанию принимается равным нулю. После достижения током значения в 10 мА, сопротивление правой ветви становится равным 101 Ом, поскольку RON=1 Ом. Ключи, управляемые током, должны иметь имена, начинающиеся с W. В команде .MODEL должна использоваться запись ISWITCH. Входной файл:

Current-Controlled Switch

i 0 1 4 0mA

VO 1 1A 0V

Ri 1A 0 100

RL 2 0 100

W 1 2 V0 W1

.MODEL W1 ISWITCH(ION=10mA RON=1 ROFF=1E6)

.DC i 0 4 0mA 1mA

.PROBE

.END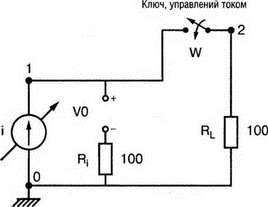

Рис. 13.12. Модель нелинейного сопротивления с ключом, управляемым током

Выполните анализ и получите график зависимости i(R_L) от тока i. Поскольку изменение сопротивления происходит в схеме плавно, график тока через R_L не имеет постоянного наклона, пока ток существенно не превышает 15 мА. Для токов в этой ветви, больших чем 15 мА, сопротивление ветви равно 101 Ом. График приведен на рис. 13.13.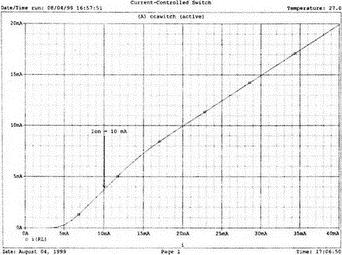

Рис. 13.13. Характеристика модели нелинейного сопротивления с ключом, управляемым током

S[имя] <+узел ключа> <-узел ключа> <+узел управления> <-узел управления> <имя модели>

Например, запись

S 2 3 1 0 S1

показывает, что управляемый напряжением ключ s включен между узлами 2 и 3. По умолчанию ключ обычно разомкнут, но когда напряжение управления (между узлами 1 и 0) достигает некоторого значения, ключ замыкается. Команда S требует включения во входной файл директивы .MODEL, чтобы определить сопротивления во включенном и выключенном состояниях и значение управляющего напряжения. В нашем примере модель идентифицируется как S₁. Запись идентификации всегда должна начинаться с символа S. Полное описание команды приведено в приложении D.

W[имя] <+узел> <-узел> <имя источника напряжения> <модель>

Например, запись

W 1 2 V0 W1

показывает, что ключ, управляемый током, включен между узлами 1 и 2. По умолчанию ключ обычно разомкнут, но когда ток управления, протекающий через ветвь, содержащую источник нулевого напряжения V0 достигает установленного значения, ключ замыкается. Команда W также требует включения во входной файл директивы .MODEL, чтобы определить сопротивления во включенном и выключенном состояниях и значение управляющего тока. В директиве .MODEL имя модели должно начинаться с символа W. Полное описание команды приведено в приложении D.

.MODEL <имя> <тип> ([<имя параметра> = <значение>]*)

Например, запись

.MODEL KT core

вводит модель для связанных катушек индуктивности, имя должно начинаться с K. Если команда также содержит слово core, то используется нелинейная модель. Кривая В(Н) для этого нелинейного устройства будет подобна показанной на рис. 13.5.

13.1. При обсуждении модели нелинейного резистора мы указали, что нелинейными являются фактически не резисторы, а зависимые источники. Измените схему, показанную на рис. 13.1, чтобы получить такое напряжение V(3), при котором мощность источника V увеличилась бы приблизительно в 1.5 раза.

13.2. Для схемы, показанной на рис. 13.14, L₁=25 мГн, С₁=C₂=50 нФ, R_s=1 Ом, R_L=1 кОм и M=1 мГн. Команда ввода для трансформатора имеет форму:

K1 L1 L2 value

где value — значение коэффициента связи. Создайте входной файл, позволяющий получить график напряжения на R_L вблизи резонансной частоты. Получите из графика коэффициент связи и сравните его с критическим значением (установите, больше он, меньше или равен критическому значению). Проверьте ваш ответ.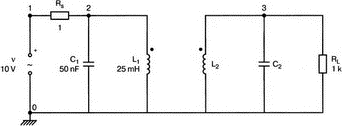

Рис. 13.14

13.3. Каково значение критического коэффициента связи в задаче 13.2? Выполните анализ, чтобы показать, что при критическом значении коэффициента связи обеспечивается максимальная передача мощности в R_L.

13.4. В схеме, показанной на рис. 13.15, используется трансформатор с ферромагнитным магнитопроводом (модель по умолчанию). Катушка индуктивности L₁ содержит 150 витков, в то время как вторичная катушка имеет 300 витков. Выполните анализ при частоте f=4,5 кГц, чтобы определить напряжение и ток резистора нагрузки.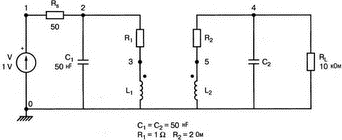

Рис. 13.15

13.5. Используйте рисунок к задаче 13.4, заменив в нем модель трансформатора двумя катушками индуктивности L₁ и L₂. Чтобы получить приблизительно те же результаты, что и прежде, задайте L₁=5 мГн и L₂=10 мГн. Проведите анализ и распечатайте переменные составляющие напряжений V(2) и V(4). Вы должны получить V(2)=0,978 В и V(4)=1,367 В. Выберите другие значения для L₁ и L₂ чтобы получить результаты, близкие к полученным в задаче 13.4. Выполните анализ несколько раз, использовав выбранные значения.

13.6. Ключ, управляемый напряжением, показан на рис. 13.9. Выберите параметры так, чтобы ключ имел сопротивление 1 кОм в разомкнутом и 1 Ом в замкнутом состояниях. Задайте R_i= 50 Ом и R_L=100 Ом. Сначала ключ должен быть замкнут. Он должен разомкнуться, когда входное напряжение v достигнет 5 В. Создайте входной файл, проведите анализ и проверьте ваши результаты по графику, полученному в Probe. 

13.7. Вернувшись к рис. 13.9, используйте значения сопротивлений, приведенные на рисунке. Ключ должен иметь сопротивление в 1 кОм в разомкнутом и 1 Ом в замкнутом состояниях. Сначала ключ должен быть замкнут. Он должен разомкнуться, когда напряжение на R_i достигнет 0,25 В. Создайте входной файл, проведите анализ и проверьте ваши результаты по графику, полученному в Probe. Обратите внимание, что в команде ввода ключа порядок следования узлов должен обеспечить правильный анализ. Выполните анализ, чтобы определить соответствующий порядок этих узлов. Вы можете быть удивлены. По графикам, полученным в Probe, убедитесь, что ток через R_i становится значительным, когда входное напряжение v превышает 0,55 В.