|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2. Анализ цепей на переменном токе (для установившихся синусоидальных режимов)Spice показывает напряжения узлов на постоянном токе без всяких специальных команд, поскольку определение напряжений постоянного тока является необходимым для получения рабочих точек в транзисторных схемах и при решении других традиционных задач. Но если вы хотите провести анализ на переменном токе, необходимо специально задать это в условиях моделирования. Вводный пример показывает, как это делается. Последовательная RL-цепочка на переменном токеПоследовательная цепь на рис. 2.1 содержит источник напряжения в 1 В, включенный последовательно с резистором R и катушкой индуктивности L. Последовательная RL-цепочка может служить, например, схемой замещения для реального дросселя. Компоненты схемы характеризуются значениями R=1,5 Ом; L=5,3 мГн и f=60 Гц. Необходимо найти ток в цепи и полное сопротивление реального дросселя. Входной файл имеет вид: AC Circuit with R and L in Series (Coil) V 1 0 AC 1V R 1 2 1.5 L 2 0 5.3mH R3 2 0 5k .AC LIN 1 60Hz 60Hz .PRINT AC I(R) IR(R) II(R) IP(R) .END 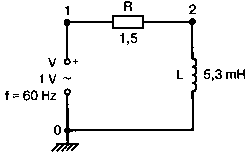 Рис. 2.1. Последовательная RL-цепь при питании от источника гармонического напряжения Команда .AC в нашем случае обеспечивает линейную вариацию значений в диапазоне от 60 до 60 Гц, то есть одну точку. Команда .PRINT предусматривает печать значений различных величин в этой точке: I(R) — амплитуда тока; IM(R) — также амплитуда тока; IR(R) — действительная часть тока; II(R) — мнимая часть тока; IP(R) — фазовый угол тока. Если Вы хотите выразить подобным образом падение напряжения V2 на индуктивности, можно записать: V(2) — амплитуда падения напряжения на индуктивности (между узлами 2 и 0 соответственно); VM(2) — также амплитуда тока этого напряжения; VR(2) — действительная часть напряжения; VI(2) — мнимая часть напряжения; VP(2) — фазовый угол напряжения. Запустите моделирование на PSpice. Узловые напряжения в выходном файле показаны как нулевые. Это означает, что они не содержат постоянных составляющих. Токи источников напряжения и мощности также не содержат постоянных составляющих (и они равны 0). Интересующая нас часть результатов моделирования дает FREQ=60 Гц для частоты и I(R)=0,4002 А для амплитуды переменного тока источника питания. Действительная часть комплексного тока равна IR(R)=0,2403 А, мнимая его часть составляет II(R)=–0,3201 А, а фазовый угол равен IP(R)=–53,1°. Задачи такого типа на переменном токе хорошо иллюстрируются векторными диаграммами (рис. 2.2). Опорное напряжение направлено под нулевым углом. Вектор тока смещен на вычисленный угол -53,1°. Можно найти также полное сопротивление реальной катушки, представленной RL-цепочкой: 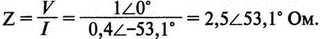 Поскольку напряжение имеет единичное значение, полученная величина идентична обратному значению вектора тока I. 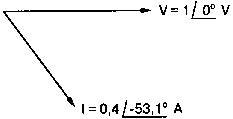 Рис. 2.2. Векторная диаграмма последовательной RL-цепи Последовательная RC-цепочка на переменном токеЗаменив в схеме на рис. 2.1 катушку индуктивности конденсатором С, получим следующую схему (рис. 2.3). Значения компонентов в этой схеме: R=5 Ом; С=100 мкФ и f=318 Гц. 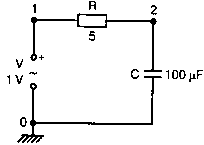 Рис. 2.3. Схема с последовательной RC-цепочкой Входной файл будет следующим: AC Circuit with Resistance and Capacitance in Series V 1 0 AC 1V R 1 2 5 С 2 0 100uF .AC LIN 1 318Hz 318Hz .PRINT AC I(R) IP(R) V(2) VP(2) .END В команде .PRINT через V(2) и VP(2) обозначены модуль и фазовый угол напряжения на конденсаторе соответственно. Запустите моделирование на PSpice и постройте векторную диаграмму тока и напряжения. Ваш рисунок должен соответствовать рис. 2.4. 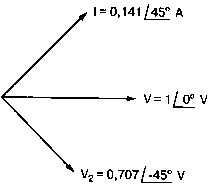 Рис. 2.4. Векторная диаграмма для последовательной RC-цепи Параллельные ветви на переменном токеРассмотрим теперь процессы в параллельной RL-цепи при питании ее от источника переменного тока (рис. 2.5). 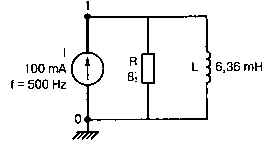 Рис. 2.5. Схема с параллельной RL-цепью Параметры компонентов: I=100∠0° мА; R=8,33333 Ом; L=6,36 мГн. Для этой цепи необходимо найти напряжение на параллельных ветвях, ток через каждую ветвь и полную проводимость цепи. Входной файл при этом имеет вид: AC Circuit with Parallel branches R and L I 0 1 AC 100 R 1 0 8.33333 L 1 0 6.36mH .AC LIN 1 500Hz 500Hz .PRINT AC V(1) VP(1) V(1) I(R) IP(R) I(L) IP(L) .END Модуль и фазовый угол напряжения представлены в выходном файле как V(I) и VP(1), а токи через отдельные ветви находятся как обычно. Запустив моделирование и получив результаты, убедитесь, что V(I)=0,7691 и VP(1)=22,64°. Проводимость RL-цепи равна Y=I/V(I)=(0,100∠0°)/(0,7691∠22,6°)=(0,13∠22,6°) С. Постройте векторную диаграмму для схемы, показав все токи и напряжение V1. Сверьте ваш результат с рис. 2.6. 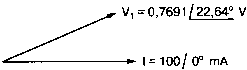 Рис. 2.6. Векторная диаграмма для параллельной RL-цепи В качестве упражнения по анализу цепей преобразуйте токи из синусоидальных в прямоугольные и сложите их. Сравните полученный результат с заданным ранее значением тока источника. Параллельная RC-цепьНа рис. 2.7 приведена схема с параллельной RC-цепью. Значения элементов этой схемы: I=100∠0° мА; R=8,33 Ом; С=14,14 мкФ и f=500 Гц. 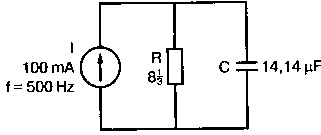 Рис. 2.7. Схема с параллельной RC-цепью Перед тем как провести моделирование на PSpice, рассчитайте полную проводимость RC-цепи. Она задается выражением Y=G+jB, где G = 1/R и В=2πfC. Входной файл имеет вид: AC Circuit with Parallel branches R and С I 0 1 AC 100 R 1 0 8.33333 N 1 0 14.14mF .AC LIN 1 500Hz 500Hz .PRINT AC V(1) VP(1) I(R) IP(R) I(C) IP(C) .END Проведите моделирование, затем постройте векторную диаграмму цепи и сравните полученный результат с приведенным на рис. 2.8. Он дает для напряжения значение V=0,7815∠–20,3° В. Проверьте вычисленное ранее значение Y, используя формулу Y= I/V. 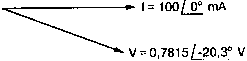 Рис. 2.8. Векторная диаграмма для параллельной RC-цепи Максимальная передача мощности в цепях переменного токаВ цепях постоянного тока максимальная мощность, выделяемая в нагрузке, достигается при RL=RS. В цепях переменного тока передача максимальной мощности достигается в том случае, когда значения полного сопротивления источника и нагрузки являются комплексно-сопряженными величинами. Например, если ZS=(600+j150) Ом, то максимальная мощность в нагрузку передается при ZL=(600–j150) Ом. Чтобы иллюстрировать это для простых последовательных цепей, на рис. 2.9 приведена схема с необходимым соотношением комплексных сопротивлений. При частоте 1 кГц реактивные сопротивления в 150 Ом получаются при индуктивности L=23,873 мГн и емкости С=1,061 мкФ. 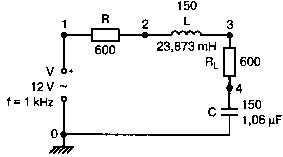 Рис. 2.9. Схема для определения максимальной мощности, выделяемой в нагрузке Входной файл имеет вид: Maximum Power Transfer in AC Circuits V 1 0 AC 12V RS 1 2 600 L 2 3 23.873mH RL 3 4 600 N 4 0 1 .06uF .OPT nopage .AC LIN 1 1 kHz 1 kHz .PRINT AC I(RL) IP(RL) V(3) VP(3) .END Maximum Power Transfer AC Circuits I 0 1 AC 100 R 1 0 8.33333 N 1 0 14.14mF .AC LIN 1 500Hz 500Hz .PRINT AC V(1) VP(1) I(R) IP(R) I(C) IP(C) .END Проведите анализ и убедитесь, что ток в цепи равен 10 мА при угле почти в ноль градусов, а амплитуда напряжения составляет V(3)=6,185 В при угле в 14,04°. Мощность, выделяемую в нагрузке, проще всего найти как Р=|I|²R=60 мВт. Резонанс в цепи наступает на частоте 1 кГц. Дальнейшее обсуждение проблемы резонанса будет продолжено в следующем разделе. В качестве самостоятельного упражнения измените значение RL до 550 Ом и проведите анализ заново. Убедитесь, что значение мощности уменьшилось по сравнению с предыдущим случаем. Повторите то же самое для сопротивления RL=650 Ом. Отметим, что при заданных значениях L и С и при изменении частоты до некоторого другого значения, значение X станет больше или меньше, а ток уменьшится. Резонанс в последовательных RLC-цепяхПоследовательный резонанс достигается в RLC-цепи, когда ее комплексное сопротивление становится чисто резистивным. При этом индуктивное и емкостное сопротивление взаимно компенсируются, ток становится максимальным, а фазовый угол — нулевым (то есть ток и приложенное напряжение находятся в фазе). Резонансная частота легко находится из уравнения: 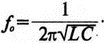 На рис. 2.10 приведена такая схема. Значения элементов: R=50 Ом; L=20 мГн и С=150 нФ. При этих параметрах резонансная частота f0=2905,81 Гц. Приложенное напряжение выбрано равным 1∠0° В. Можно работать со следующим входным файлом: Series Resonance with RLC V 1 0 AC 1V R 1 2 50 L 2 3 20mH C 3 0 150nF .AC LIN 4901 100Hz 5kHz .PROBE .END 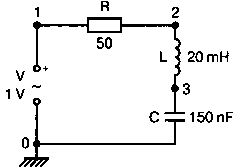 Рис. 2.10. Последовательная резонансная RLC-цепь Команда .АС предусматривает линейную вариацию частоты от 100 Гц до 5 кГц, содержащую 4901 шаг, один шаг для каждого целочисленного значения частоты в этом диапазоне. После выполнения PSpice анализа в программе Probe будут построены графики для частот от 100 Гц до 10 кГц. Могут быть получены различные графики для сложных функций параметров схемы. Сделайте следующее: 1. Постройте график зависимости IP(R) для линейного частотного диапазона от 2 до 4 кГц (эта зависимость называется фазочастотной характеристикой — ФЧХ). Для этого выберите Trace, Add Trace…, введите с клавиатуры необходимую переменную IP(R) в поле Trace Expression и нажмите OK. Чтобы получить желательный диапазон по оси X выберите Plot, Axis Settings… и в поле X-axis выберите User Defined с диапазоном от 2 до 4 кГц. Затем выберите Scale Linear и OK. Если при выводе кривой вы получаете ошибку, выберите Trace, Delete All Traces и повторите процесс, чтобы получить необходимую кривую. Ваш график должен пройти через ноль при частоте, близкой к 2,9 кГц. Проверьте это, выбирая режим курсора (он имеет символ, который напоминает пересекающиеся пунктиры и символ проверки), затем, используя мышь или стрелки ← → на клавиатуре, найдите положение «нулевого сдвига фаз», которое должно соответствовать частоте f=2,0058 кГц (см. рис. 2.11); 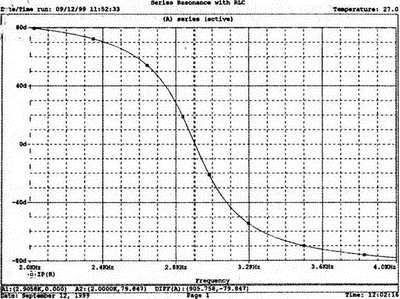 Рис. 2.11. Фазочастотная характеристика резонансного RLC-контура 2. Получите в программе PROBE график V(1)/I(R) для того же частотного диапазона от 2 до 4 кГц. Для этого сначала выберите Trace, Delete All Traces и затем — Trace, Add Trace, как вы делали прежде. Диапазон по оси Y должен быть от 0 до 300. Используйте Trace, Cursor, Display mode, чтобы найти следующие значения: при f=2 кГц, Z=283,6 Ом; при f=2,9 кГц, Z=50 Ом; и при f=4 кГц, Z=242,6 Ом; 3. Удалите эту кривую, и получите на экране сразу два графика: напряжения V(3) и тока I(R). Используйте операции Plot, Add Plot to Window, чтобы получить вторую кривую. Измените частотный диапазон в пределах от 0 до 5 кГц. В результате максимум для V(3) должен составлять приблизительно 7,3 В, а для I(R) –20 мА. Проверьте эти значения с помощью ручного расчета и сравните с рис. 2.12. 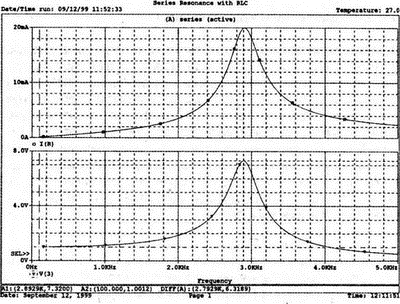 Рис. 2.12. Амплитудно-частотные характеристики тока и напряжения на конденсаторе для RLC-контура Частотный анализ в последовательно-параллельных цепях переменного токаНа рис. 2.13 приведена еще одна цепь на переменном токе. Значения параметров: V=100∠0° В; R1=10 Ом; R2=10 Ом, L=100 мГн и С=10 мкФ. Предположим, что резонансная частота неизвестна, и ее необходимо предварительно определить. 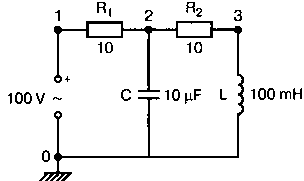 Рис. 2.13. Последовательно-параллельная схема Входной файл можно записать в виде: Series-Parallel AC Circuit V 1 0 AC 100V R1 1 2 10 R2 2 3 10 L 3 0 100mH C 3 0 10uF .AC LIN 100 50Hz 1000Hz .PRINT AC I(R1) IP(R1) .END При записи команды .АС мы предположили, что резонансная частота лежит в диапазоне от 50 до 1000 Гц. Если ее значение лежит за пределами этого диапазона, можно изменить диапазон частот в команде. Команда .PRINT выводит в выходном файле величины модуля и фазового угла для тока схемы. Поскольку нулевому фазовому углу соответствует коэффициент мощности, равный единице, при анализе нетрудно отыскать соответствующую частоту. Проведите моделирование на PSpice, и проанализируйте выходной файл. Не поленитесь распечатать файл, так как вам придется изменять диапазон частот. Вы должны подтвердить, что резонанс происходит между значениями f=155 Гц и f=165 Гц. Для этого измените во входном файле, диапазон частот с помощью команды .AC LIN 101 100 200 Теперь мы рассматриваем все целочисленные значения частот между 100 и 200 Гц. Выполнив анализ, мы увидим, что резонанс происходит между частотами 158 Гц и f= 159 Гц и ток вблизи резонанса равен приблизительно 98 мА. Этот пример позволяет оценить преимущества моделирования на PSPICE. Происходит ли резонанс при частоте, предсказываемой известной формулой .AC LIN 51 155Hz 160Hz Она обеспечивает шаг по частоте в 0,1 Гц. Проведите моделирование снова и найдите частоту, при которой изменяется знак фазового угла IP(R1). Результат должен показать, что она лежит в диапазоне 158,3 и 158,4 Гц. Из нашего моделирования следует, что приведенная выше формула резонанса неправильна для исследуемой последовательно-параллельной схемы. Обратите внимание, что минимум тока приходится не на резонансную частоту, а на частоту f=159,2 Гц, при которой фазовый угол тока составляет приблизительно 5,97°. Интересным упражнением для вас должна стать замена команды .PRINT командой .PROBE в этом анализе. При этом результаты проведенного нами численного анализа будут наглядно представлены на графике. Преимуществом графического представления результатов кроме наглядности является возможность получения частотных зависимостей для многих величин без изменения входного файла. Влияние изменения сопротивления катушкиНа рис. 2.13 одна из параллельных ветвей содержит R=10 Ом и L=100 мГн. Эта цепь может служить моделью реальной катушки с малым сопротивлением. Интересно, как влияет сопротивление катушки на поведение схемы? Изменим входной файл, установив R2=50 Ом, и заметим, что при этом f0=138 Гц. Затем установим R2=80 Ом и увидим, что f0=95 Гц. Предполагали ли вы, что изменение резонансной частоты будет столь велико? Посмотрите, как легко PSpice позволяет Вам изменять параметры схемы и формировать новый набор исходных условий для вычисления. При этом команда .PRINT обеспечивает высокую точность вычислений, а команда .PROBE неоценима для того, чтобы увидеть графические зависимости для переменных. Параллельные резонансные цепиУравнения для анализа параллельной резонансной цепи значительно сложнее уравнений для последовательного колебательного контура. Можно найти полное описание этих уравнений в учебниках. Однако моделирование на PSpice позволяет легко находить резонансную частоту и полное входное сопротивление такой схемы при резонансе. В этом примере вы можете снова использовать курсор в программе Probe. Схема, показанная на рис. 2.14, содержит ветвь с катушкой и ветвь с конденсатором. Значения параметров элементов схемы: RL=10 Ом; L=2,04 мГн; RC=5 Ом и С=0,65 мкФ. Отметим, что включение резистивного датчика тока сопротивлением R=1 Ом последовательно в цепь источника напряжения V превращает его в неидеальный источник с напряжением 1 В. Предварительный анализ показывает, что резонансная частота лежит между 4 и 5 кГц. 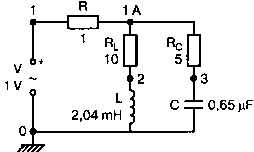 Рис. 2.14. Параллельная резонансная цепь Входной файл приведен ниже: Parallel Resonant Circuit V 1 0 AC 1V RL 1A 2 10 RC 1A 3 5 R 1 1A 1 L 2 0 2.04mH C 3 0 0.65uF .AC LIN 1001 4000Hz 5000Hz .PROBE .END Во входном файле задано изменение частоты от 4 до 5 кГц с шагом в 1 Гц. Выполните анализ, затем, используя возможности Probe, получите график IP(R). Диапазон частот выведенного графика по оси X лежит в пределах от 1 до 10 кГц, предусматривая логарифмическую шкалу. Это означает, что выбранная кривая занимает лишь малую часть экрана. Выберите для шкалы по оси X линейный масштаб и диапазон от 4 до 5 кГц. Как и ожидалось, резонансная частота имеет значение, близкое к 4,3 кГц, что видно из графика на рис. 2.15. 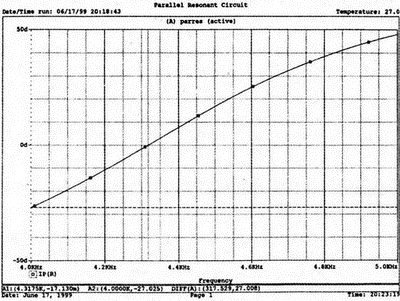 Рис. 2.15. Фазочастотная характеристика для схемы на рис. 2.14 Использование курсора в программе ProbeИз строки меню выберите Trace, Cursor, Display, и на экране появится поле Probe Cursor. Оно может появиться в правой нижней части, но его при желании можно переместить и в другую область экрана. Поле содержит следующую информацию: А1 = 4.0000K, -27.025 А2 = 4.0000K, -27.025 dif = 0.000, 0.000 Строка А1 представляет значения X и Y: частоты и величины фазового угла тока IP(R) в левом конце графика. Частота равна 4 кГц, а фазовый угол составляет -27,025, то есть при f=4 кГц вектор тока повернут на -27,02° относительно вектора входного напряжения, фазовый угол которого считается нулевым. Клавишей стрелки (→) переместите указатель курсора до отметки, где фазовый сдвиг будет нулевым (или почти нулевым). После этого значения на табло Probe Cursor изменятся А1 = 4.3175K, -17.130m А2 = 4.0000K, -27.025 dif = 3ъ17.544, 27.010 Полученные вами значения могут несколько отличаться. На самом деле, если вы удалите график и снова получите его, значения могут немного измениться, так как используется подпрограмма итераций, чтобы достигнуть необходимой точки графика. Строка A1 сообщает, что при f=4,3175 кГц фазовый угол тока близок к нулю. Таким образом, резонансная частота f0=4,3175 кГц, так как при этом входной ток находится в фазе с приложенным напряжением. Сопротивление R в схеме необходимо, чтобы сделать источник входного напряжение реальным источником напряжения. Интересно определить также полное входное сопротивление (или полную проводимость) схемы при резонансе. Убедитесь еще раз, что сопротивление (или проводимость) при резонансе должны быть полностью активными (не должны содержать реактивной составляющей). Постройте с учетом этого график I(R). Поскольку V=1 В, ток схемы численно равен полной входной проводимости. Объясните, почему это так. Используйте снова режим курсора для этого графика. Перемещайте указатель курсора, пока не найдете предсказанную частоту f0=4,3175 кГц. Каково значение тока I на этой частоте? Убедитесь, что I=4,683 мА при резонансной частоте. Убедитесь также, что Z0=R0=213,5 Ом. Отметьте, что ток при этом не минимален. Определение полного входного сопротивления в цепях переменного токаРассмотрим «черный ящик», содержащий цепь с неизвестным полным сопротивлением, показанный на рис. 2.16. С помощью команды .PRINT вы можете вывести и V(I), и I(R). Однако эта команда не позволяет вывести значение V(I)/I(R). Различные математические операторы в ней не допускаются. Чтобы получить график желаемой переменной, следует использовать функцию Probe, которая может, кроме того, строить функции, использующие следующие операторы:
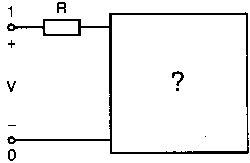 Рис. 2.16. Чёрный ящик, содержащий цепь с неизвестным полным сопротивлением Таким образом, чтобы найти входное полное сопротивление схемы (рис. 2.16), можно включить очень маленький резистор R в качестве датчика тока. Полное входное сопротивление V(1)/I(R) можно найти в Probe, используя выражения r(V(I)/I(R)) для вещественной части Z и img(V(I)/I(R)) для мнимой части. Это дает тот же результат, что и использование r(VM(I)/IM(R)) и img(VM(I)/IM(R)). Получить фазовый угол для Z можно, используя p(V(I)/I(R)). Поясним эту методику примером. На рис. 2.17 показана схема с резистивным датчиком тока и «неизвестным» полным сопротивлением в «черном ящике». Чтобы найти полное сопротивление, необходимо провести моделирование и использовать Probe. 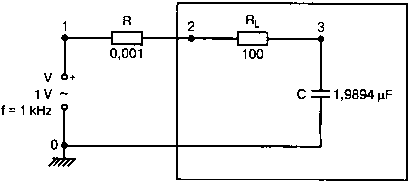 Рис. 2.17. Схема с резистивным датчиком тока Во входном файле предусмотрена вариация частоты входного напряжения: Input Impedance Using a Small Current-Sensing Resistor V 1 0 AC 1V R 1 2 0.001; Это резистивный датчик тока (шунт) RL 2 3 100 RA 1 1А 1 С 3 0 1.9894uF .AC LIN 501 500Hz 1500Hz .PROBE .END Проведите моделирование, и получите в Probe графики частотных зависимостей для действительной и мнимой частей Zin. Результаты показаны на рис. 2.18. Используя режим курсора, убедитесь, что при f=1 кГц получаются следующие значения сопротивления: Rin=100 Ом (действительная часть Zin) и Xin=-80 Ом (мнимая часть Zin). 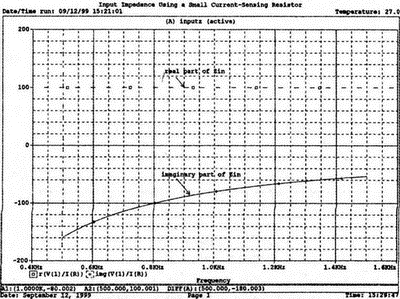 Рис. 2.18. Частотные зависимости для активной и реактивной составляющих Zin Полное входное сопротивление в цепях с двумя ветвямиВ предыдущей схеме результаты достаточно просто можно было найти и без использования Probe. В более сложной схеме (рис. 2.19) найти полное входное сопротивление вручную достаточно трудно. При использовании же Probe результаты получаются так же просто, как и для предыдущей схемы. Входной файл для этого случая: Input Impedance of Two-Branch Network V 1 0 AC 12V Rs 1 2 50; Это резистивный датчик тока (шунт) R1 2 3 100 R2 3 5 80 R3 3 4 75 R4 5 6 60 L 4 0 15.92mH C 6 0 3.183uF .AC LIN 501 500Hz 1500Hz .PROBE .END 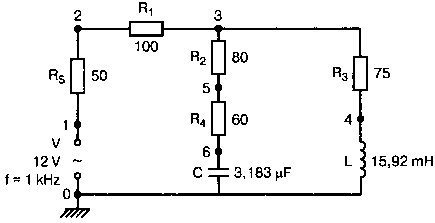 Рис. 2.19. Схема с двумя ветвями для расчета полного входного сопротивления Используя возможности Probe, найдите полное входное сопротивление (для части схемы справа от узла 2) при частоте f=1 кГц. Убедитесь, что Zin=(178,9+j29,33) Ом. Если вы предпочитаете записывать действительную и мнимую составляющие просто в форме упорядоченной пары, то запись будет иметь вид Zin=(178,9; 29,33) Ом. Сравните полученные вами графики с графиком на рис. 2.20. 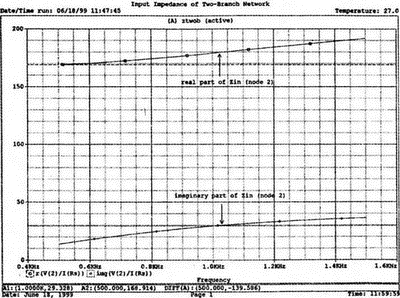 Рис. 2.20. Частотные зависимости для активной и реактивной составляющих Zin в схеме на рис. 2.19 Фазосдвигающие цепиПростая фазосдвигающая цепь, использующая только конденсаторы и резисторы, показана на рис. 2.21. Это мостовая Т-образная схема со следующими параметрами элементов: С1=С2=10 нФ; R1=200 Ом; R2=250 Ом; RL=100 Ом и R=1 Ом (резистивный датчик тока). С помощью PSpice-анализа можно определить фазосдвигающие свойства этой цепи. Определите, при какой частоте фазовый сдвиг тока относительно входного напряжения максимален и какова его величина в этой точке. Подберите эмпирически диапазон частот для такого анализа. 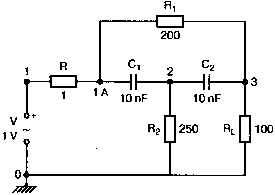 Рис. 2.21. Фазосдвигающая цепь Входной файл имеет вид: Phase-Shift Network V 1 0 AC 12V R 1 1А 1 R1 1A 3 200 R2 2 0 250 RL 3 0 100 C1 1A 2 10nF C2 2 3 10nF .AC LIN 501 5kHz 500kHz .PROBE .END Проведите анализ на PSpice, затем получите график IP(R), используя линейную шкалу частот в диапазоне от 5 до 500 кГц. Легко установить, что максимальный сдвиг фазы немного меньше 30° и приходится на частоту около 300 кГц. Воспользовавшись режимом курсора, получим более точные значения: максимальный сдвиг фазы 29,67° при f=281,4 кГц. Не выходя из Probe, получите график IP(RL). Он непосредственно покажет сдвиг фазы в Т-образной схеме. Найдите частоту, при которой схема имеет нулевой сдвиг фазы. Обратите внимание, что это происходит при частоте менее 50 кГц. С учетом этого измените входной файл, установив диапазон частот от 5 до 50 кГц. Выполните анализ снова и определите частоту для нулевого сдвига фазы с помощью графика IP(RL). Воспользовавшись курсором, убедитесь, что f=29,32 кГц. Ваш график должен быть похож на приведенный на рис. 2.22. 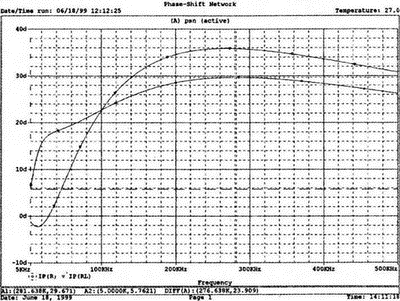 Рис. 2.22. Частотные характеристики фазосдвигающей цепи Частотные зависимости полных проводимостейГрафическая методика, которая часто используется в схемотехническом анализе на переменном токе, основана на нахождении годографов полных сопротивлений или полных проводимостей. Если элементы включены последовательно, складываются частотные зависимости полных сопротивлений участков цепи и находится общая частотная зависимость. Если элементы включены параллельно, те же операции производятся для проводимостей отдельных ветвей. Схема на рис. 2.23 содержит две параллельные ветви с параметрами: С=0,318 мкФ; RL=50 Ом и L=3,18 мГн. Во входном файле задан диапазон частот от 5 Гц до 10 кГц: Locus of Admittances V 1А 0 AC 1V R 1 1A 1 RL 1 2 50 L 2 0 3.18mH C 1 0 0.318 uF .AC LIN 201 5Hz 10kHz .PROBE .END 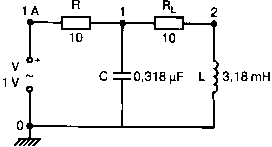 Рис. 2.23. Схема для определения фазовых траекторий проводимости Выполните анализ и выведите график IP(R), чтобы найти резонансную частоту. Воспользовавшись курсором, убедитесь, что f0=4,336 кГц. Теперь измените шкалу по оси X так, чтобы это позволило представить полную проводимость во всем диапазоне. Поскольку V=1 В, Y=I/V=I/1. Таким образом, проводимость Y численно равна току, и вы можете заменять график I графиком Y и наоборот. Вы можете получить также зависимость B(G), где активная составляющая проводимости G откладывается по горизонтальной, а реактивная составляющая B — по вертикальной оси. Координаты точек такого графика представляют собой действительную и мнимую составляющие вектора проводимости, а совокупность точек служит годографом вектора проводимости при изменении частоты. Прежде чем пытаться изменить масштаб по оси X, удалите кривые, имеющиеся на экране, и выберите Plot, Axis Settings…, опции Auto Range, Linear, затем нажмите кнопку Axis Variable. Для выбора функции введите с клавиатуры «IR(R)» и дважды щелкните OK. Затем получите график II(R). Поскольку I и Y численно равны, можно считать, что по осям отложены действительная G (ось X) и мнимая В (ось Y) составляющие, а весь график рассматривать как годограф проводимости (Y-plane). График содержит важную информацию, которая видна не сразу. Верхний левый конец кривой соответствует частоте f=10 кГц. При перемещении точки вниз вправо уменьшается частота, при которой могут быть получены соответствующие значения В и G. Переместив курсор в точку, где В=0 (примерно), вы увидите, что при этом G=5 мС. Вследствие этого полное сопротивление цепи при резонансной частоте 4,336 кГц равно 200 Ом. Распечатайте годограф проводимости. Отметьте ось Х как G (в мС) и ось Y как В (также в мС) для дальнейшего изучения. Ваш график должен быть похож на график, приведенный на рис. 2.24. 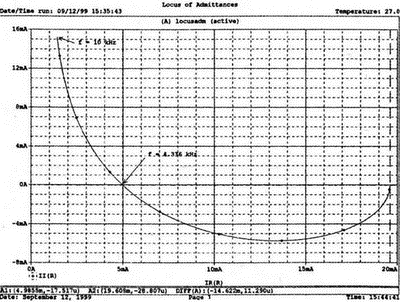 Рис. 2.24. Годограф полной проводимости для схемы на рис. 2.23 Вы знаете, где размещены на этом графике две частоты, но как вы можете идентифицировать другие? Простой метод состоит в том, чтобы изменить во входном файле верхнюю границу частоты в команде вариации частоты. Для начала установите ее равной 6 кГц и снова выполните моделирование. Получив значения карты проводимости, запомните, где начинается график (6 кГц), и отметьте эту точку на предыдущем графике, пользуясь значениями G и В. Сделайте это несколько раз для других значений верхней границы, отмечая каждое новое положение точки значением f на первоначальном графике. Годограф проводимости для последовательного RLC-контураИнтересная форма годографа проводимости получается для последовательного RLC-контура. Можете вы предсказать, на что она будет похожа? Если масштаб для B и G будет одинаковым, она будет окружностью. Параметры элементов в схеме, приведенной на рис. 2.25: R=50 Ом; L=20 мГн и С=150 нФ. Соответствующий входной файл: Admittance Locus for Series RLC Circuit V 1 0 AC 1V R 1 250 L 2 3 20mH С 3 0 150nF .AC LIN 5001 1000Hz 10kHz .PROBE .END 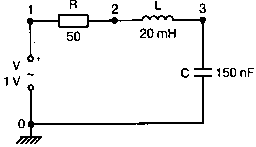 Рис. 2.25. Последовательная цепь для определения полной проводимости Резонансная частота соответствует крайней правой точке и составляет 2906 Гц. В программе Probe необходимо выбрать Plot, Axis Settings…, на табло X Axis — User Defined, ввести значения «0А» в 20 мА, Scale Linear, затем нажать кнопку Axis Variable и для Trace Expression: набрать TR(R) и нажать OK. Выполните анализ и получите график II(R). Кривая начинается с нижней частотной границы в левой части экрана и при повышении частоты точка перемещается по часовой стрелке по овальной траектории. При перемещении с позиции 9 часов в позицию 3 часа проходится диапазон частот от 0 Гц (наш график фактически начинается при f=100 Гц) до резонансной частоты 2906 Гц. Вся нижняя половина круга приходится на диапазон от резонансной частоты до верхнего частотного предела в 10 кГц. Распечатайте график для дальнейшего изучения. Обратите внимание, что вид графика к окружности можно менять соответствующим выбором границ на осях X и Y, хотя при этом можно потерять некоторую часть круга на экране или распечатанной копии. Этот график показан на рис. 2.26. 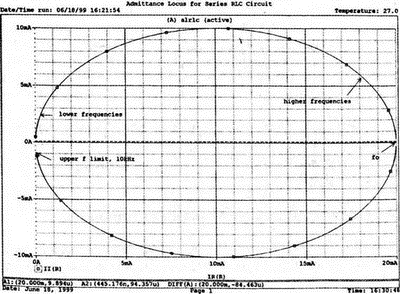 Рис. 2.26. Годограф проводимости для последовательного RLC-контура Теперь удалите график, и выберите в качестве переменной по оси X частоту. Использование курсора для графика I(R) в функции частоты позволяет найти резонансную частоту. Цепи переменного тока с несколькими источникамиКогда в схеме переменного тока имеется более одного источника питания, вы должны определить относительные фазовые углы источников. Обратите внимание, что в каждой команде, описывающей источник напряжения в примере на рис. 2.27, значение напряжения сопровождается значением фазового угла. Так, V2, амплитуда которого составляет 10 В, а начальный угол -90°, записывается как 10V-90. Ваше задание в этом примере состоит в том, чтобы найти ток через каждый из элементов С, L, и R и напряжение V(2). Входной файл: AC Network with More Than One Source V1 1 0 AC 20V 0 V2 0 4 AC 10V -90 V3 3 0 AC 40V 45 R 2 4 3 L 2 3 7.96mH С 1 2 663uF .AC LIN 1 60Hz 60Hz .print ac i(C) iR(C) ii(C) ip(C) .print ac i(L) iR(L) ii(L) ip(L) .print ac i(R) iR(R) ii(R) ip(R) .print ac v(2) vR(2) vi(2) vp(2) .opt nopage .end 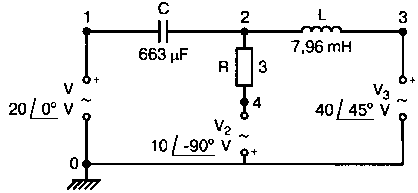 Рис. 2.27. Схема с тремя источниками переменного напряжения Выполните моделирование в PSpice, и рассмотрите результаты, полученные в выходном файле. Каковы направления токов, которые были найдены? Чтобы понять это, вы должны учитывать описание элементов во входном файле. Например, команда, описывающая конденсатор, вводит узлы в последовательности 1, 2. Это означает, что на диаграмме цепи вы должны показать ток в направлении из узла 1 к узлу 2. Если вы этого не сделаете, решение будет неоднозначным. При просмотре команд для R и L, проставьте стрелки с направлением тока для этих элементов, чтобы получить однозначное решение. Рассмотрим выходной файл на рис. 2.28. Обратите внимание, что не интересующие нас в данном случае строки были удалены при редактировании. Это полезная практика при распечатке таких файлов. **** 08/17/05 18:26:07 ******** Evaluation PSpice (Nov 1999) AC Network with More Than One Sources **** CIRCUIT DESCRIPTION V1 1 0 AC 20V 0 V2 0 4 AC 10V -90 V3 3 0 AC 40V 45 R 2 4 3 L 2 3 7.96mH C 1 2 663uF .AC LIN 1 60Hz 60Hz .print ac i(C) iR(C) ii(C) ip(C) .print ac i(L) iR(L) ii(L) ip(L) .print ac i(R) iR(R) ii(R) ip(R) .print ac v(2) vR(2) vi(2) vp(2) .opt nopage .end **** AC ANALYSIS TEMPERATURE = 27.000 DEG C FREQ I(C) IR(C) II(C) IP(C) 6.000E+01 2.050E+00 8.907E-01 -1.846E+00 -6.424E+01 6.000E+01 8.243E+00 -8.238E+00 2.994E-01 1.779E+02 6.000E+01 9.377E+00 9.129E+00 -2.145E+00 -1.323E+01 6.000E+01 2.762E+01 2.739E+01 3.564E+00 7.414E+00 Рис. 2.28. Выходной файл для схемы на рис. 2.27 Трехфазные сети будут рассматриваться в следующем разделе. Исходные напряжения будут определены таким же способом, как в представленном примере. ТрансформаторыПри использовании трансформаторов в Spice необходимо при вводе этого элемента задать коэффициент самоиндукции каждой из двух обмоток (первичной и вторичной) и коэффициент связи k. На рис. 2.29 показана схема с источником напряжения 20 В частотой 1 кГц. Для трансформатора заданы следующие параметры: R1=20 Ом; L1=25 мГн; R2=20 Ом; L2=25 мГн и взаимная индуктивность М=20 мГн. Найдите токи в первичной и вторичной обмотках, мощность вторичной обмотки и мощность в полном сопротивлении нагрузки. 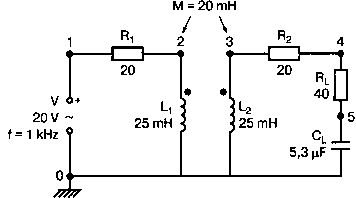 Рис. 2.29. Схема со взаимной индуктивностью Коэффициент связи может быть найден из уравнения: 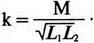 Для примера, это значение будет равно 20/25 или 0,8. Теперь вы готовы создать входной файл: Circuit with Mutual Inductance V1 1 0 AC 20V 0 R1 1 2 20 R2 3 4 20 L1 2 0 25mH L2 3 0 25mH RL 4 5 40 CL 5 0 5.3uF K L1 L2 0.8 .AC LIN 1 1kHz 1kHz .print ас i(R1) iR(R1) ii(R1) .print ac i(R2) iR(R2) ii(R2) .opt nopage .end Выполните анализ и распечатайте копию выходного файла. Убедитесь, что первичный ток равен (0,1767–0,1441), а вторичный ток составляет (0,1979–0,04904) А. Обратите внимание, что эти ответы даны просто как упорядоченные пары для реальных и мнимых компонентов. Результаты не дают желательных мощностей непосредственно, так как команды .PRINT не могут содержать выражений типа I*I*R. Используйте калькулятор, чтобы проверить, что мощность вторичной обмотки равна 2,49 Вт, а мощность полного сопротивления нагрузки — 1,66 Вт. В некоторых трансформаторных схемах важно обозначить начала обмоток (обычно они обозначаются точками). В этом примере точками обозначены начало первичной обмотки L1, подключенное к узлу 2, и начало вторичной обмотки L2, подключенное к узлу 3. Таким образом, точками отмечены узлы, указанные первыми для каждой индуктивности L. Реакция в частотной области для цепей настройки частотыСхемы настройки используются в различных электронных устройствах, которые находят применение в радио и телевидении. Параллельно трансформаторным обмоткам подключаются конденсаторы, чтобы создать резонансные контуры. Вблизи резонансной частоты во вторичный контур передается большая мощность, при удалении от резонансной частоты эта мощность падает. На рис. 2.30 показана типовая схема, питающаяся от источника переменного тока: I=19,6 мА; R1=R2=1 Ом; L1=L2=25 мГн; C1=С2=1,013 мкФ; RL=5 кОм и k=0,05. Резонансная частота LC-цепи составляет f0=1 кГц. 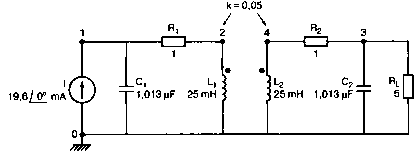 Рис. 2.30. Схема подстройки частоты с индуктивной связью Интересно исследовать поведение схемы при частотах, близких к резонансной. Это можно осуществить, используя следующий входной файл: Frequency Response of Tuned Circuit with Mutual Inductance I 0 1 AC 19.6mA R1 1 2 1 R2 3 4 1 L1 2 0 25mH L2 4 0 25mH RL 3 0 5k K L1 L2 0.05 C1 1 0 1.013uF C2 3 0 1.013uF .AC LIN 401 800Hz 1200Hz .PROBE .END Будем изменять частоту в диапазоне от 800 до 1200 Гц. Проведите анализ и получите график V(3) в этом диапазоне частот. Используя линейную шкалу по оси X, исследуйте форму напряжения на нагрузке. Обратите внимание, что оно повышается с обеих сторон от резонансной частоты. Распечатайте полученный график для дальнейшего изучения (см. рис. 2.31). 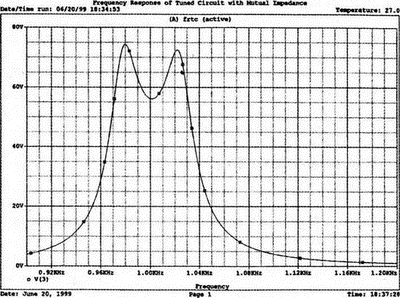 Рис. 2.31. Амплитудно-частотная характеристика подстроечного контура Величина k, равная 0,05 в этом примере, называется коэффициентом связи. Она определяет используемую полосу частот, в которой мощность передается с небольшим ослаблением. Когда напряжение падает ниже 0,7 от максимального значения, мы выходим за границы пригодной для использования полосы частот. Можете вы определять ширину полосы частот для данной схемы подстройки? Воспользуйтесь курсором, чтобы проверить, что V(3)=74,321 В и f=980 Гц в точке максимума. 70 % от этого значения составляют 52 В; этот уровень достигается при частотах f1=970 Гц, f2=1032 Гц, давая ширину полосы пропускания BW=62 Гц. Задайте во входном файле новое значение k=0,03. Выполните моделирование снова и обратите внимание, что пик стал выше, а ширина полосы пропускания уменьшилась. В этом случае пик V(3)=82,156 В, самое большое пиковое значение напряжения на нагрузке будет достигнуто при значении k, дающем критическую связь (для этой схемы при k=0,0155). Выполните моделирование, еще раз при этом значении k. Убедитесь, что в максимуме V(3)=99,238 В. Трехфазные цепи переменного токаТрехфазные схемы переменного тока могут быть рассчитаны по той же методике, что и однофазные, если нагрузка в каждой фазе одинакова (симметричная нагрузка). Когда нагрузка несимметрична, решение становится более сложным. В этом примере приводится метод решения для случая несимметричной нагрузки (рис. 2.32). 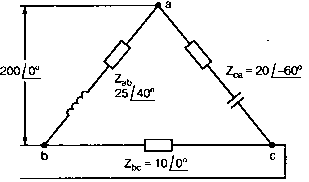 Рис. 2.32. Схема несимметричной трехфазной нагрузки В этой задаче полные сопротивления ветвей нагрузки, включенной по схеме треугольника, равны: Zab=25∠40° Ом; Zbc=10∠0° Ом и Zca=20∠-60° Ом. Линейные напряжения равны 200 В при частоте 60 Гц. Фазовый угол для Vab равен 0°, и используется прямая последовательность фаз. Это означает, что Vab=200∠0° В, Vbc=200∠-120° В и Vca=200∠120° В. Начните решение с определения значений L и С. Они легко находятся вручную при известных значениях полных сопротивлений и частоты. Включите в ветви источников питания маленькие сопротивления, хотя в условии задачи они отсутствуют. Если этого не сделать, PSpice даст сообщение об ошибках, указывающее наличие петли напряжений. Сопротивления в линии включены, чтобы позволить вам находить линейные токи. На рис. 2.33 показана скорректированная схема. Входной файл для нее будет иметь вид: Three Phase Unbalanced Load VAB 12 2 AC 200V 0 VBC 20 0 AC 200V -120 VCA 10 1 AC 200V 120 RS1 12 1 0.01 RS2 20 2 0.01 RS3 10 0 0.01 RA 1 3 0.01 RB 2 4 0.01 RC 0 5 0.01 RAB 3 34 19.15 LAB 34 4 42.627mH RBC 4 5 10 RCA 3 35 10 CCA 35 5 153.15uF AC LIN 1 60Hz 60Hz .print ac i(RA) iP(RA) iR(RA) ii(RA) .print ac i(RB) iP(RB) iR(RB) ii(RB) .print ac i(RC) iP(RC) iR(RC) ii(RC) .opt nopage .end 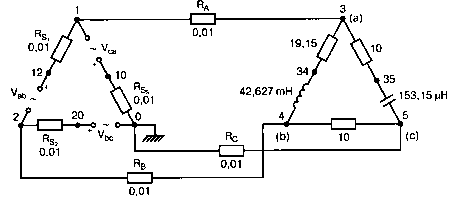 Рис. 2.33. Схема на рис. 2.32, скорректированная для проведения анализа на PSpice Выполните анализ на PSpice и проверьте токи, показанные в выходном файле на рис. 2.34. Например, I(RA)=(16,09∠-5,136)=16,89 -17,7° А. Обратите внимание, что величина тока, обозначенная в выходном файле как I(RA), могла бы также быть определена как IM(RA). Покажите направления для каждого из токов на вашей схеме; без этого решение остается неопределенным. В качестве проверки добавьте линейные токи, чтобы видеть, что их сумма равна нулю. Учтите, что в результатах могут быть небольшие ошибки округления. Three Phase Unbalanced Load **** CIRCUIT DESCRIPTION VAB 12 2 AC 200V 0 VBC 20 0 AC 200V - -120 VCA 10 1 AC 200V 120 RS1 12 1 0.01 RS2 20 2 0.01 RS3 10 0 0.01 RA 1 3 0.01 RB 2 4 0.01 RC 0 5 0.01 RAB 3 34 19.15 LAB 34 4 42.627mH RBC 4 5 10 RCA 3 35 10 CCA 35 5 153.15uF .AC LIN 1 60Hz 60Hz .print ac i(RA) iP(RA) iR(RA) ii(RA) .print ac i(RB) iP(RB) iR(RB) ii(RB) .print ac i(RC) iP(RC) iR(RC) ii(RC) . opt nopage .end **** AC ANALYSIS TEMPERATURE = 27.000 DEG С FREQ I(RA) IP(RA) IR(RA) II(RA) 6.000E+01 1.639E+01 -1.770E+01 1.609E+01 -5.136E+00 FREQ I(RB) IP(RB) IR(RB) II(RB) 6.000E+01 2.016E+01 -1.430E+02 -1.609E+01 -1.215E+01 FREQ I(RC) IP(RC) IR(RC) II(RC) 6.000E+01 1.728E+01 9.001E+01 -3.292E-03 1.728E+01 Рис. 2.34. Выходной файл для схемы на рис. 2.33 Исправление коэффициента мощностиТок, потребляемый асинхронным двигателем, можно снизить, подключив к сети конденсатор. Проведем некоторые предварительные вычисления, рассматривая асинхронный двигатель в 5 лошадиных сил, который потребляет 53 А при 117 В при КПД 78,5 %. Входная мощность двигателя равна: 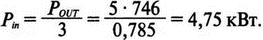 Полная мощность равна: S = VI = 117·53 = 6,2 кВ·А. По известным значениям Р и S можно найти реактивную мощность Q из треугольника мощностей: S = P + JQ. что дает для реактивной мощности Q = 3,985 кВАР. Сопротивление двигателя равно: 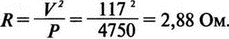 Реактивное сопротивление двигателя равно: 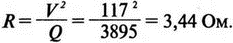 При частоте f=60 Гц это соответствует индуктивности 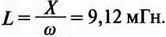 После решения задачи вручную может показаться, что здесь не требуется анализ на PSpice. Однако компьютерный анализ будет полезен, чтобы увидеть влияние подключения линейных конденсаторов. Обратимся к рис. 2.35, на котором показаны R и L для двигателя, наряду с двумя резистивными датчиками RA и RB. Их роли станут очевидными, когда мы добавим в схему конденсатор. 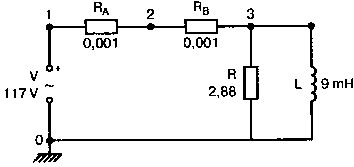 Рис. 2.35. Схема для анализа улучшения коэффициента мощности Необходимо получить входной файл, который покажет общий ток и токи ветвей в зависимости от приложенного напряжения: Single-Phase Motor, 5 hp V 1 0 AC 117V RA 1 2 0.01 RB 2 3 0.01 R 3 0 2.88 L 3 0 9.12mH .AC LIN 1 60Hz 60Hz .print ac i(RA) iP(RA) i(RB) iP(RB) .print ac i(R) iP(R) .print ac i(L) iP(L) .opt nopage .end Выходной файл покажет следующие значения токов: I(RA)=5.263Е+01, IP(RA)= -3.962Е+01 I(RB)=5.263E+01, IP(RB)= -3.962E+01 I(R) =4.034E+01, IP(R) = 3.310E-01 Значение линейного тока I(RA) близко к рассчитанному значению 53 А при фазовом угле, близком -40°. Коэффициент мощности pf (power factor) найден как косинус угла между векторами линейного тока и линейного напряжения: pf = cos(-40°) = 0,76. Сумма векторов токов ветвей (токи через R и L двигателя) равна линейному току. Теперь просто показать эффект подключения конденсатора между линиями (между узлами 2 и 0). Добавим во входной файл команду С 2 0 380uF и изменим одну из команд печати, чтобы включить в выходной файл ток через конденсатор. Теперь выполните анализ снова. Выходной файл покажет следующее: I(RA) = 4.411Е+01, IP(RA) =-2.299Е+01 I(RB) = 5.296Е+01, IP(RB) = -3.993Е+01 I(C) = 1.676Е+01, IP(C) = 9.001Е+01 I(R) = 4.060E+01, IP(R) = 2.510E-02 I(L) = 3.401E+01, IP(L) = -8.997E+01 Мы видим, что линейный ток I(RA) уменьшился до 44,11 А при отстающем угле ≈23°, ясно показывая эффект повышения коэффициента мощности. Коэффициент мощности теперь равен pf = cos(-23°) = 0,92. Конденсатор проводит ток 16,76 А с фазовым углом 90°, вызывая изменение линейного тока. Обратите внимание, что ток через резистор датчика RB равен прежнему значению линейного тока, как и следовало ожидать. Исправление коэффициента мощности в трехфазных цепях На рис. 2.36 компонентами, показанными справа, представлен трехфазный двигатель, включенный по схеме треугольника. Компоненты R1, и L1 — это, соответственно, сопротивление и индуктивность двигателя «на фазу». Другие фазы имеют те же значения компонентов. 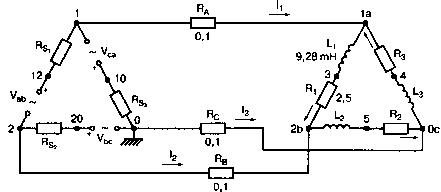 Рис. 2.36. Трехфазный двигатель, подключенный по схеме треугольника В каждую из линий трехфазной сети включены резисторы, понижающие линейное напряжение. Во входной файл включены команды, обеспечивающие вывод различных напряжений и токов. Он показан в составе выходного файла на рис. 2.37. Circuit for Power-Factor correction VAB 12 2 AC 240V 0 VBC 20 0 AC 240V - -120 VCA 10 1 AC 240V 120 RS1 12 1 0.01 RS2 20 2 0.01 RS3 10 0 0.01 RA 1 3 0.01 RB 2 4 0.01 RC 0 5 0.01 R1 3 2B 2.5 R2 5 0С 2.5 R3 4 1A 2.5 L1 1A 3 9.28MH L2 2B 5 9.28MH L3 0С 4 9.28MH .AC LIN 1 60HZ 60HZ .PRINT AC I(RA) IP(RA) .PRINT AC I(RB) IP(RB) .PRINT AC I(RC) IP(RC) .PRINT AC I(R1) IP(R1) .PRINT AC I(R2) IP(R2) .PRINT AC I(R3) IP(R3) .PRINT AC V(1A, 2B) VP(1A,2B) .PRINT AC V(2B,0C) VP(2B,0C) .PRINT AC V(0C,1A) VP(0С,1А) .OPT NOPAGE .END FREQ I(RA) IP(RA) 6.000E+01 9.615E+01 -8.402E+01 FREQ I(RB) IP(RB) 6.000E+01 9.615E+01 1.560E+02 FREQ I(RC) IP(RC) 6.000E+01 9.615E+01 3.598E+01 FREQ I(R1) IP(R1) 6.000E+01 5.551E+01 -1.140E+02 FREQ I(R2) IP(R2) 6.000E+01 5.551E+01 5.981E+00 FREQ I(R3) IP(R3) 6.000E+01 5.551E+01 1.260E+02 FREQ V(1A,2B) VP(1A,2B) 6.000E+01 3.220E+02 -1.316E+02 FREQ V(2B,0C) VP(2B,0C) 6.000E+01 3.220E+02 -1.157E+01 FREQ V(0C,1A) VP(0С,1А) 6.000E+01 3.220E+02 1.084E+02 Рис. 2.37. Выходной файл для анализа схемы на рис. 2.36 Обратите внимание на порядок следования индексов в каждой инструкции. Для каждого пассивного элемента индексы находятся в соответствии с направлениями токов, показанными на рис. 2.36. Векторная диаграмма токов и напряжений показана на рис. 2.38. Угол между напряжением фазы V(1a, 2b) и током фазы I(R1) равен: 3,22+51,23=54,45°. Ток отстает от напряжения на 54,45°. Косинус этого угла — коэффициент мощности pf = cos(-54,45°) = 0,581. 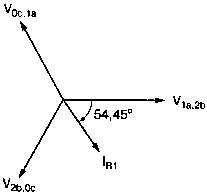 Рис. 2.38. Векторная диаграмма токов и напряжений в схеме на рис. 2.36 Мы собираемся улучшить коэффициент мощности, включив в схему батарею конденсаторов, как показано на рис. 2.39. Изменим входной файл, чтобы показать присутствие конденсаторов. После выполнения анализа на PSpice результаты должны быть такими, как показано на рис. 2.40. 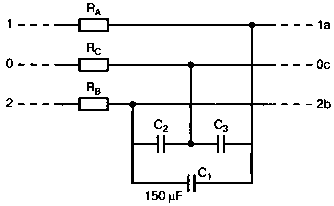 Рис. 2.39. Схема питания трехфазного двигателя с конденсаторами для исправления коэффициента мощности Circuit for Power-Factor correction VAB 12 2 AC 240V 0 VBC 20 0 AC 240V -120 VCA 10 1 AC 240V 120 RS1 12 1 0.01 RS2 20 2 0.01 RS3 10 0 0.01 RA 1 3 0.01 RB 2 4 0.01 RC 0 5 0.01 R1 3 2B 2.5 R2 5 0C 2.5 R3 4 1A 2.5 L1 1a 3 9.28mH L2 2b 5 9.28mH L3 0c 4 9.28mH C1 la 2b 150uF C2 2b 0c 150uF C3 0c 1a 150uF .AC LIN 1 60HZ 60HZ .PRINT AC I(RA) IP(RA) I(C1) IP(C1) .PRINT AC I(RB) IP(RB) I(C2) IP(C2) .PRINT AC I(RC) IP(RC) I(C3) IP(C3) .PRINT AC I(R1) IP(R1) .PRINT AC I(R2) IP(R2) .PRINT AC I(R3) IP(R3) .PRINT AC V(1A,2B) VP(1A,2B) .PRINT AC V(2B, 0C) VP(2B,0C) .PRINT AC V(0C,1A) VP(0С,1A) .OPT NOPAGE .END FREQ I(RA) IP(RA) I(C1) IP(C1) 6.000E+01 9.257E+01 -9.335E+01 2.152E+01 -6.090E+01 FREQ I(RB) IP(RB) I(C2) IP(C2) 6.000E+01 9.257E+01 1.467E+02 2.152E+01 5.910E+01 FREQ I(RC) IP(RC) I(C3) IP(C3) 6.000E+01 9.257E+01 2.665E+01 2.152E+01 1.791E+02 FREQ I(R1) IP(R1) 6.000E+01 4.749E+01 -1.470E+02 FREQ I(R2) IP(R2) 6.000E+01 4.749E+01 -2.704E+01 FREQ I(R3) IP(R3) б.000E+01 4.749E+01 9.296E+01 FREQ V(1A,2B) VP(1A,2B) 6.000E+01 3.806E+02 -1.509E+02 FREQ V(2B,0C) VP(2B,0C) 6.000E+01 3.806E+02 -3.090E+01 FREQ V(0С,1A) VP(0С,1A) 6.000E+01 3.806E+02 8.910E+01 Рис. 2.40. Выходной файл с результатами анализа схемы на рис. 2.39 Мы видим, что каждый из линейных токов уменьшился после включения в схему конденсаторов с 92,64 до 75,51 А. Уменьшение тока сопровождается улучшением коэффициента мощности. Коэффициент мощности найдем по прежней методике. Напряжение фазы примем равным V(1a, 2b)=230∠2,26° В, ток фазы найдем (косвенно) из тока I(RA)=75,52∠-72,2° А. Так как это линейный ток, соответствующий ток фазы имеет величину 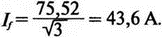 при фазовом угле –42,2°. Этот угол мы получили, прибавив 30° к углу линейного тока. И величина и угловые значения справедливы для симметричной нагрузки. Угол коэффициента мощности равен 2,26°+42,2°=44,46°. Коэффициент мощности: pf = cos (-44,46°) = 0,581Р = 0,71. При несимметричных нагрузках применяется другой подход к нахождению тока фазы, при котором складываются ток в одной фазе нагрузки и соответствующий ток в конденсаторе. Таким образом, складывая I(R1) и I(С1), мы получаем: I(R1) + I(C1) = 53,53∠-52,19° + 13,02∠92,226° = 43,6∠-42,18° A. в соответствии с предыдущими вычислениями. В отсутствие конденсаторов коэффициент мощности составлял 0,58. В случае необходимости можно легко выполнить анализ на PSpice с другими значениями емкости для сравнения. Трехфазный выпрямительНа рис. 2.41 показан трехфазный выпрямитель, соединенный в звезду. Все фазные напряжения имеют максимальное значение 10 В при частоте 60 Гц. Схема обеспечивает режим без пауз тока в нагрузке. Входной файл: Three-Phase Rectifier v1 1 0 sin(0 10V 60Hz 0 0 0) v2 2 0 sin(0 10V 60Hz 0 0 -120) v3 3 0 sin(0 10V 60Hz 0 0 120) DA 1 4 D1 DB 2 4 D1 DC 3 4 D1 RL 4 0 100 .MODEL D1 D .TRAN 0.1us 33.33ms .PROBE .END 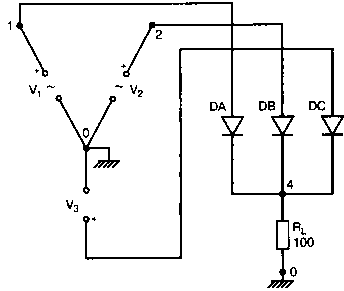 Рис. 2.41. Трехфазный выпрямитель Выполните анализ, воспользовавшись программой Probe, и проверьте результаты, показанные на рис. 2.42. Затем удалите графики напряжений и получите график тока нагрузки I(RL). Убедитесь, что он изменяется между минимальным значением 43,5 мА и максимальным значением 92,3 мА. 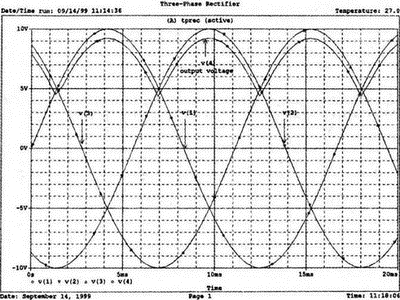 Рис. 2.42. Форма напряжений в схеме на рис. 2.41, полученная в программе Probe Команда .MODEL используется, чтобы описать диод. Диод один из многих приборов, поддерживаемых PSpice. Имя DI определяется нашим выбором, но буква D в начале обозначения требуется всегда и не может быть заменена другой. Команды, вводящие три одинаковых диода, устанавливают, что DA, DB и DC основаны на том же самом типе диода, который мы применяли ранее для DI. Для других примеров обратитесь к приложению В. Регулировка напряжения в трехфазных системахМощная фидерная линия должна быть спроектирована так, чтобы падение напряжения между источником и нагрузкой не превышало предельного значения. Часто разрешается использовать падение напряжения для регулировки напряжения на нагрузке в пределах 5 или менее процентов. Схема на рис. 2.43 используется, чтобы иллюстрировать требования к регулированию напряжения. Мы видим, что в каждую линию включены сопротивление и индуктивность. Будет ли желательное регулирование напряжения достигнуто при R=0,077 Ом и L=0,244 мГн в линии фидера? Воспользуемся моделированием PSpice, чтобы найти напряжение на нагрузке. 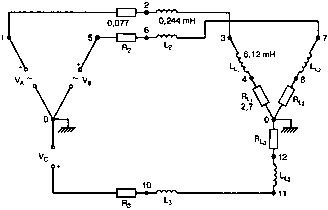 Рис. 2.43. Схема для иллюстрации регулирования напряжения Нагрузка, соединенная в звезду, представляет собой трехфазный двигатель, предназначенный для питания от сети 440 В, 60 Гц. Исходное линейное напряжение составляет 460 В, откуда фазное напряжение: 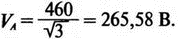 Входной файл не требует никаких дополнительных пояснений. Он показан на рис. 2.44 вместе с результатами анализа. Процент регулирования напряжения ΔV равен: 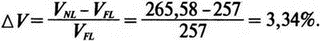 Voltage Regulation for Three-Phase Load VA 1 0 AC 265.58V 0 VB 5 0 AC 265.58V -120 VC 9 1 AC 265.58V 120 R1 1 2 0.077 R2 5 6 0.077 R3 9 10 0.077 L1 2 3 0.244mH L2 6 7 0.244mH L3 10 11 0.244mH RL1 4 0 2.7 RL2 8 0 2.7 RL3 12 0 2.7 LL1 3 4 6.12mH LL2 7 8 6.12mH LL3 11 12 6.12mH .AC LIN 1 60HZ 60HZ .PRINT AC I(R1) IP(R1) I(R2) IP(R2) .PRINT AC I(R3) IP(R3) .PRINT AC V(3) VP(3) V(7) VP(7) .PRINT AC V(11) VP(11) .OPT NOPAGE .END **** AC ANALYSIS TEMPERATURE = 27.000 DEG С FREQ I(R1) IP(R1) I(R2) IP(R2) 6.000E+01 7.237E+01 -4.083E+01 7.237E+01 -1.608E+02 FREQ I(R3) IP(R3) 6.000E+01 7.237E+01 1.917E+01 FREQ V(3) VP(3) V(7) VP(7) 6.000E+01 2.570E+02 -3.108E-01 2.570E+02 -1.203E+02 FREQ V(11) VP(11) 6.000E+01 2.570E+02 5.969E+01 Рис. 2.44. Выходной файл при моделировании схемы на рис. 2.43 Двухфазные системыПроведем анализ двухфазной системы, скорее всего, для удовлетворения собственного любопытства, пользуясь тем, что его очень легко реализовать на PSpice. На рис. 2.45 приведена такая схема, где полные сопротивления нагрузки равны Z=(25+j50) Ом для каждой фазы. 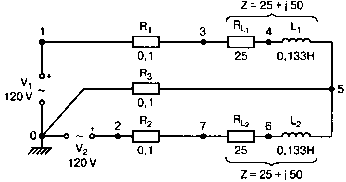 Рис. 2.45. Двухфазная схема Two-Phase System V1 1 0 AC 120 0 V2 2 0 AC 120 -90 R1 1 3 0.10 R2 2 7 0.10 R3 0 5 0.10 RL1 3 4 25 RL2 7 6 25 L1 4 5 0.133H L2 6 5 0.133H .AC LIN 1 60HZ 60HZ .PRINT AC V(3,5) VP(3,5) .PRINT AC V(7,5) VP(7,5) .PRINT AC I(RL1) IP(RL1) .PRINT AC I(RL2) IP(RL2) .PRINT AC I(R3) IP(R3) .OPT NOPAGE .END **** AC ANALYSIS TEMPERATURE = 27.000 DEG С FREQ V(3,5) VP(3,5) 6.000E+01 1.200E+02 2.284E-01 FREQ V(7,5) VP(7,5) 6.000E+01 1.196E+02 -8.986E+01 FREQ I(RL1) IP(RL1) 6.000E+01 2.142E+00 -6.327E+01 FREQ I(RL2) IP(RL2) 6.000E+01 2.135E+00 -1.534E+02 FREQ I(R3) IP(R3) 6.000E+01 3.022E+00 7.178E+01 Рис. 2.46. Выходной файл с результатами анализа схемы на рис. 2.45 При частоте 60 Гц, реактивное сопротивление 50 Ом соответствует индуктивности L=0,133 Гн. Входной файл включен в рис. 2.46, который показывает выходные напряжения и токи. Фазные напряжения на нагрузке имеют почти одинаковые значения (120 В) и сдвинуты приблизительно на 90°. Линейные токи I(RL1) и I(RL2) также имеют почти равные значения (2,15 А) и сдвинуты приблизительно на 90°. Обратите внимание на ток I(RL1), сдвинутый на угол -63,27°, который является также фазовым углом для полного сопротивления нагрузки. Ток нейтрали I(R3) более чем в два раза превышает линейные токи: Z = R + jXL = 25 + j50 = 55,9∠63,4°Ом. Нарисуйте векторную диаграмму, показав фазные напряжения на нагрузке и каждый из трех линейных токов. Интересно посмотреть, что получится, если увеличить сопротивление в каждой линии. Установим для R1, R2 и R3 значения сопротивлений в 10 Ом и выполним моделирование снова. Новый выходной файл показан на рис. 2.47. Обратите внимание, что V(3,5)=111∠19,3° и V(7,5)=89,1∠-82,2°. Напряжения теперь несбалансированы и сдвинуты на 105,5°. Линейные токи также несбалансированы, и снова ток нейтрали больше, чем любой из двух других токов. Two-Phase System with Large Values of Line Resistance V1 1 0 AC 120 0 V2 2 0 AC 120 -90 R1 1 3 10 R2 2 7 10 R3 0 5 10 RL1 3 4 25 RL2 7 6 25 L1 4 5 0.133H L2 6 5 0.133H .AC LIN 1 60HZ 60HZ .PRINT AC V(3,5) VP(3,5) .PRINT AC V(7,5) VP(7,5) .PRINT AC I(RL1) IP(RL1) .PRINT AC I(RL2) IP(RL2) .PRINT AC I(R3) IP(R3) .OPT NOPAGE .END **** AC ANALYSIS TEMPERATURE = 27.000 DEG С FREQ V(3,5) VP(3,5) 6.000E+01 1.110E+02 1.926E+01 FREQ V(7,5) VP(7,5) 6.000E+01 8.909E+01 -8.220E+01 FREQ I(RL1) IP(RL1) 6.000E+01 1.981E+00 -4.424E+01 FREQ I(RL2) IP(RL2) 6.000E+01 1.590E+00 -1.457E+02 FREQ I(R3) IP(R3) 6.000E+01 2.280E+00 9.265E+01 Рис. 2.47. Выходной файл с результатами анализа схемы на рис. 2.45 при увеличенных сопротивлениях Обзор новых команд PSpice, применяемых в данной главеС[имя] <+узел> <-узел> <значение> Например, запись С 4 5 0.5uF показывает, что конденсатор емкостью 0,5 мкФ включен между узлами 4 и 5. При другой форме ввода в конце строки добавляется запись значения IС для того, чтобы ввести начальное значение напряжения на конденсаторе. Например, запись С 4 5 0.5uF IС 5 3V показывает, что на конденсаторе имеется начальное напряжение в 3 В, причем положительный потенциал на узле 4. I[имя] <+узел> <-узел> АС <амплитуда> [<фаза>] Например, запись IS 1 2 АС 0.35 45 указывает, что источник переменного тока 350 мА включен между узлами 1 и 2 и его начальный фазовый угол равен 45°. Помните, что значения токов и напряжений по умолчанию задаются для постоянного тока. В иных случаях это должно быть специально указано (как в нашем случае записью АС). K[имя] L [имя] L [имя] <значение коэффициента связи> Например, K L1 L2 0.1 указывает, что схема с индуктивной связью, возможно, трансформатор, имеет две связанные катушки индуктивности L1 и L2. Коэффициент связи k=0,1. Другая форма этой команды, которая касается схемы с индуктивной связью на магнитном сердечнике, будет представлена позже. L[имя] <+узел> <-узел> <значение> Например, запись L1 3 0 2 5mH указывает, что катушка индуктивности 25 мГн включена между узлами 3 и 0. Чтобы показать начальный ток, используйте IС значение в конце строки. V[имя] <+узел> <-узел> АС <амплитуда> [<фаза>] Например, запись V2 4 1 АС 110 120 указывает, что источник переменного напряжения амплитудой 110 В с фазовым углом 120 включен между узлами 4 и 1. Команды, начинающиеся с точки, используемые в данной главе.AC [LBS] [ОСТ] [DEC] <точки> <f start> <f end> Например, запись .AC DEC 2 0 1kHz 1MEG указывает, что PSpice будет выполнять моделирование с частотой в качестве переменной. Частотный диапазон — от 1 кГц до 1 МГц — использует 20 точек на декаду. Если выбрана опция LIN (вместо опции DEC), значение числа точек представляет общее количество точек в частотном диапазоне. .MODEL <название> <тип> [<param> = <значение>] < toI]>] Эта команда может использоваться для модели любого из элементов, доступных в PSpice: резисторов, катушек индуктивности, конденсаторов, диодов, транзисторов (биполярных или полевых) и других устройств. Имя элемента для диода должно начинаться с D и может быть DI, D2, DA, и так далее. Тип прибора должен быть выбран из приведенных в разделе .MODEL приложения В: например, RES для резистора, IND для катушки индуктивности и D для диода. .PRINT <[DC] [AC] [NOISE] [TRAN]> <output variable list> Например, при использовании команды .PRINT AC V(2) V(5,4) VP(5,4) I(R1) IP(R1) в выходном файле, использующем показанные значения для переменного тока, будут выведены следующие величины: V(2) даст величину V2; V(5,4) даст величину V54; I(R1) будет давать величину тока через резистор R1 и IP(R1) даст угол фазы тока через R1. Обратите внимание, что должен быть выбран один (и только один) из пунктов в списке DC, AC, NOISE и TRAN. .PROBE Эта команда описывалась в главе 1, но здесь приводится более подробное описание. Когда Вы включаете команду .Probe во входной файл и выполняете моделирование на PSpice, наряду с файлом данных будет создан выходной файл. Выходной файл — это текстовый файл с расширением *.out, а файл данных имеет расширение *.dat. Это не текстовый файл, но он содержит информацию, необходимую программе Probe, чтобы построить желательные графики. Другой файл с расширением *.prb содержит текст, который необходимо направить в программу Probe. Программа Probe начинается автоматически, когда команда .Probe включена в схемный файл. Появившийся экран содержит главное меню со следующими пунктами: File Edit View Simulation Trace Plot Tools Window Help Оно сопровождается двумя строками пиктограмм, которые могут использоваться вместо меню для таких функций, как открытие файлов, печать графиков, нахождение максимальных и минимальных значений и других. Первое, что необходимо сделать в Probe, это выбрать Trace, Add Trace, затем выбирать переменные из списка Simulation Output Variables в столбце слева. Столбец справа содержит список Functions или Macros. Если вы получили график, который необходимо сохранить, выберите File, Print, чтобы получить, отпечатанную версию экрана. Графики, приведенные в этой книге, были получены таким способом. Любой лазерный принтер, например один из серии HP Laser Jet фирмы HEWLETT-PACKARD, может распечатать график. Менее удовлетворительные результаты могут быть получены с некоторыми струйными принтерами типа HEWLETT-PACKARD DeskJet. Задачи2.1. Найти эквивалентное полное сопротивление схемы, показанной на рис. 2.48 со стороны источника. Так как индуктивные и емкостные сопротивления даны в омах, используйте частоту f=5 кГц, чтобы найти значения L и С, необходимые во входном файле. Проверьте ваши результаты, с помощью стандартных методов расчета схемы. 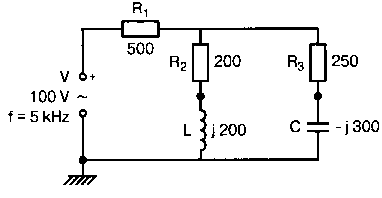 Рис. 2.48 2.2. Схема, показанная на рис. 2.49, имеет низкую добротность. Найдите резонансную частоту с помощью частотных характеристик в диапазоне от 3 до 6 кГц. Проверьте что f0=3,56 кГц. Найдите ток при резонансе и минимальный ток. Какой частоте соответствует минимальный ток? 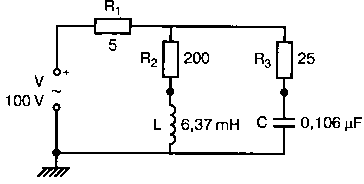 Рис. 2.49 2.3. Решите задачу 2.2 при значении R2=20 Ом. 2.4. В этой задаче исследуются изменения напряжения на R, L, и С вблизи резонанса. Параметры элементов показаны на рис. 2.50, f0=159,15 Гц. Сформируйте входной файл так, чтобы получить графики VR, VL и VC для частотного диапазона от 10 до 300 Гц. Покажите, что VRmax соответствует частоте f0 в то время как VLmax — ниже f0, a VCmax — выше f0. 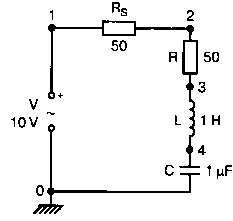 Рис. 2.50 2.5. Для схемы, показанной на рис. 2.51, найдите полное сопротивление со стороны источника при f=1 кГц. 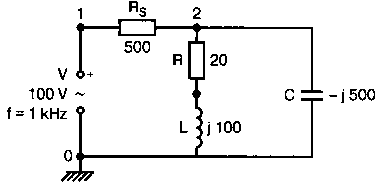 Рис. 2.51 2.6. Определите график изменения проводимостей для типичной схемы с двумя параллельными ветвями (рис. 2.52). Она подобна схеме, рассмотренной в примере данной главы. Проведите моделирование с использованием Probe и получите график IP(R), чтобы определить резонансную частоту. Затем получите карту проводимостей и найдите значения G и В при резонансе. 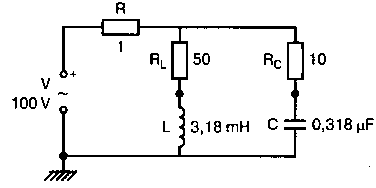 Рис. 2.52 2.7. Для схемы на рис. 2.53 найдите частоту, при которой V2=0,707 В для объяснения амплитудно-частотной характеристики (характеристики Боде) для V2/V1. Определите фазовый сдвиг при этой частоте. 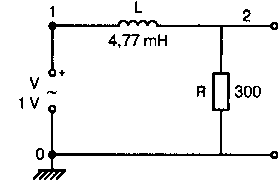 Рис. 2.53 2.8. Для схемы на рис. 2.54 найдите частоту, при которой выходное напряжение минимально, и значение напряжения при этой частоте (амплитуду и фазу). Найдите полосу частот, в которой выходное напряжение изменяется на 3 дБ или больше. 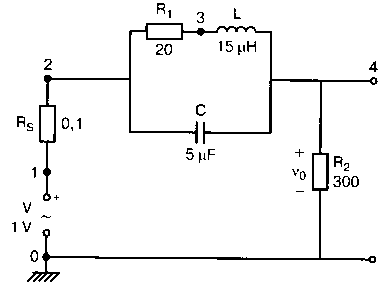 Рис. 2.54 2.9. На рис. 2.55 приведена схема с двойным резонансом. Она имеет ширину полосы пропускания в 150 кГц. Получите графики для схемы, которые подробно показывают амплитуду и фазу выходного напряжения в интересующей нас области. 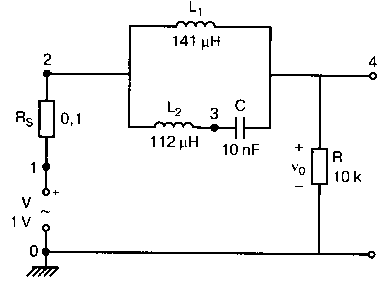 Рис. 2.55. 2.10. Для схемы на рис. 2.56 найти I1, I2 и напряжение V40 при частоте ω=1000 рад/с. Подсказка: так как значения реактивных сопротивлений не могут использоваться в PSpice непосредственно, рассчитайте значения L и С. 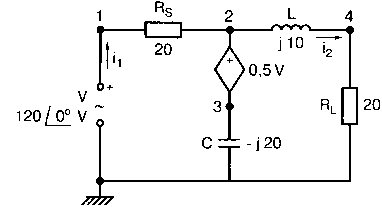 Рис. 2.56 2.11. Чтобы проверить ответы, полученные в задаче 2.10, найдите V20, затем используйте напряжение на L, чтобы найти ток i2. Сравните эти значения с результатами, полученными при решении задачи 2.10. 2.12. Для схемы, показанной на рис. 2.57, найдите i и V2. Преобразуйте источники тока в источники напряжения и проверьте ваши результаты с помощью ручного расчета. 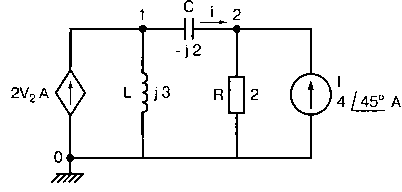 Рис. 2.57 2.13. На рис. 2.58 показана схема индикатора последовательности фаз. R1 и R2 — сопротивления идентичных ламп накаливания. Даны значения: частота f=60 Гц, V12=100∠0° В и V23=100∠–120° В. Покажите с помощью анализа на PSpice, что последовательность фаз (которая, очевидно, является прямой ABC) может быть определена по относительной яркости ламп R1 и R2. 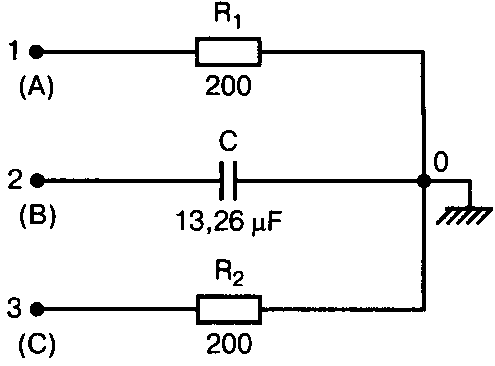 Рис. 2.58 2.14. Трехфазная несимметричная нагрузка, соединенная в звезду, подключена к симметричному трехфазному источнику питания с частотой 60 Гц: VAB=208∠0°, VBC=208∠-120° В и VCA=208∠120° В, полные сопротивления фазы ZA0=8∠30° Ом, ZB0=4∠-50° Ом, и ZCO=6∠20° Ом. Найдите три линейных тока и ток нейтрали. Подсказка: Из заданных полных сопротивлений определите значения X и R; затем преобразуйте каждое реактивное сопротивление X в L или С в зависимости от знака реактивного сопротивления. Убедитесь, что для фазы A: R=6,928 Ом и L=10,61 мГн; для фазы B: R=2,571 Ом, С=865,7 мкФ, а для фазы С: В=5,638 Ом и L=5,433 мГн. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||

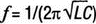 ? Вычислите это значение частоты с помощью калькулятора. Оно должно быть f=159,155 Гц. Это не совпадает с нашим предположением, что f0 находится между 158 и 159 Гц. Является ли различие просто ошибкой округления? Изменим команду во входном файле:
? Вычислите это значение частоты с помощью калькулятора. Оно должно быть f=159,155 Гц. Это не совпадает с нашим предположением, что f0 находится между 158 и 159 Гц. Является ли различие просто ошибкой округления? Изменим команду во входном файле: