• Главная
• В избранное
• Наш E-MAIL
• Добавить материал
• Нашёл ошибку
• Вниз

Операционный усилитель (ОУ), или op amp, представляет собой интегральную схему, широко используемую в электронике. Реальная схема усилителя сложна и нет необходимости отражать все ее свойства в нашей модели. Мы начнем с модели идеального ОУ, содержащей лишь наиболее существенные компоненты.

Идеальный ОУ будет смоделирован для PSpice как усилитель с высоким входным сопротивлением, нулевым выходным сопротивлением и высоким коэффициентом усиления по напряжению. Типичные значения этих параметров показаны на рис. 5.1, где R_i=1 ГОм; А=200000 и v₀=A(v₂–v₁). Обратите внимание, что напряжение v₁ относится к инвертирующему входу, a v₂ — к неинвертирующему. Эта модель будет служить для анализа на постоянном токе и при низкой частоте. При необходимости мы будем изменять модель, учитывая другие свойства ОУ.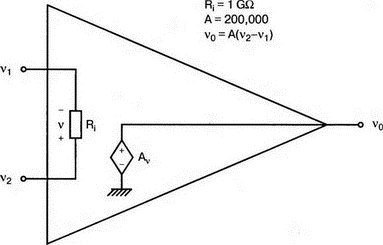

Рис. 5.1. Идеальный операционный усилитель

Хотя в применении PSpice для анализа простых схем на ОУ нет необходимости, желательно посмотреть, какую информацию дает программа даже в этих ситуациях. Имеются также некоторые ограничения, которые заслуживают нашего внимания. 

На рис. 5.2, а показана схема включения ОУ с использованием отрицательной обратной связи по напряжению. Резистор обратной связи R₂ включен между выходом и инвертирующим входом, при этом неинвертирующий вход заземлен. На рис. 5.2, б приведен вариант такой схемы для PSpice.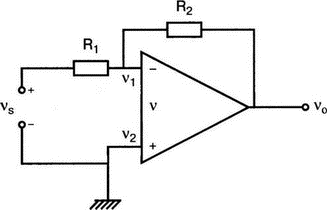

(а)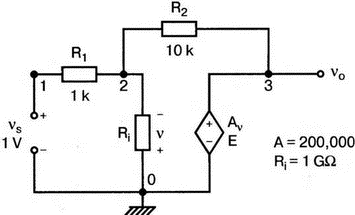

(b)

Рис. 5.2. Усилитель с отрицательной обратной связью по напряжению на базе идеального ОУ: а) схема усилителя; б) модель усилителя для PSpice

Входной файл для анализа схемы:

Ideal Operational Amplifier

VS 1 0 1V

E 3 0 0 2 200ЕЗ

R1 2 0 1G

R1 1 2 1k

R2 3 2 10k

.OP

.OPT nopage

.TF V(3) VS

.END

Проведите анализ и рассмотрите результаты, полученные в выходном файле. Убедитесь, что V(3)/VS=-9,999. Коэффициент усиления очень близок к -10 и может быть приближенно аппроксимирован выражением v₀/v_s=–R₂/R₁. Используя метод узловых потенциалов, запишите уравнения, необходимые, чтобы получить значение v₀/v_s. Убедитесь, что результаты зависят от значения А и что аппроксимация верна только тогда, когда А приближается к бесконечному значению.

В результате анализа должно получиться значение входного сопротивления R_in=1 кОм. Можете вы это объяснить? Не забудьте, что мы можем считать оба входа ОУ заземленными, и при этом входное сопротивление оказывается равным R₁.

На рис. 5.3 показана другая простая схема на ОУ. В ней напряжение v_s подключено к неинвертирующему (+) входу. На рис. 5.4 показана модель и приведены параметры элементов.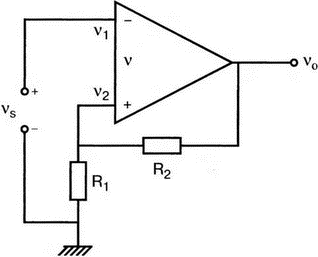

Рис. 5.3. Неинвертирующий усилитель на базе идеального ОУ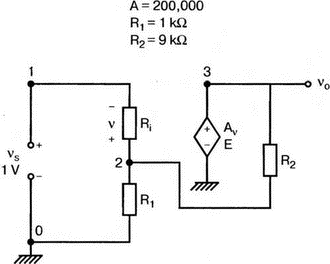 

Рис. 5.4. Модель неинвертирующего усилителя на базе идеального ОУ

Входной файл для этого случая:

Ideal Operational Amplifier, Noninverting

VS 1 0 1V

E 3 0 1 2 200E3

RI 1 2 1G

R1 2 0 1k

R2 3 2 9k

.OP

.OPT nopage

.TF V(3) VS

.END

Убедитесь, что V(3)/VS=10 в соответствии с формулой v₀/v_s=-R₂/R₁ и R_in=2,0Е13. Почему настолько велико входное сопротивление? Так как идеальный ОУ почти не потребляет тока, источник сигнала v_s работает практически в режиме холостого хода.

Если входной сигнал подается между инвертирующим и неинвертирующим входами, на выходе ОУ получается усиленная разность входных напряжений. Чтобы упростить анализ, примем, что на рис. 5.5 R_i=R₃=5 кОм и R₂=R₄=10 кОм. Модель PSpice для идеального ОУ с внешними элементами приведена на рис. 5.6. Входной файл имеет вид:

Op Amp Giving Voltage Difference Output

VA 1 0 3V

VB 4 0 10V

E 5 0 3 2 200E3

RI 2 3 1G

R1 1 2 5k

R2 5 2 10k

R3 4 3 5k

R4 3 0 10k

.OP

.OPT nopage

.TF V(5) VB

.END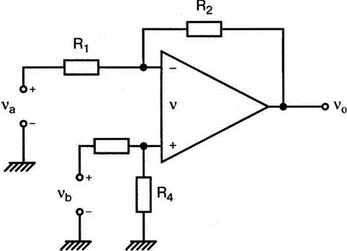

Рис. 5.5. Усилитель с дифференциальным входом на базе идеального ОУ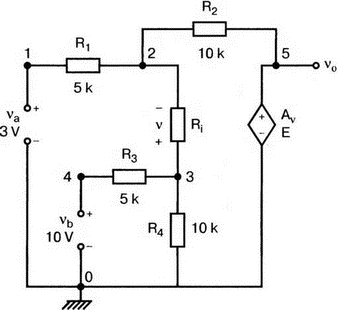

Рис. 5.6. Модель усилителя с дифференциальным входом на базе идеального ОУ

Анализ показывает, что выходное напряжение V(5)=14 В. Используя метод узловых потенциалов для анализа идеального ОУ, убедитесь, что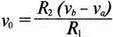

согласуется с нашими результатами. Вычисления, проведенные вручную, помогут лучше понять работу схемы. Начните с определения напряжения на неинвертирующем входе ОУ. Его легко определить, если вы вспомните, что входы ОУ не потребляют тока. Напряжение v_b подается на делитель напряжения и на его выходе получается напряжение v⁺=6,667 В, это означает, что также составляет 6,667 В (фактически PSpice дает 6,666 В). При использовании этого напряжения вы можете легко найти токи через R₁ и R₂. Выходной файл показан на рис. 5.7.

**** 07/02/99 16:11:55 ******** Evaluation PSpice (Nov 1998) *********

Op Amp Giving Voltage Difference Output

**** CIRCUIT DESCRIPTION

VA 1 0 3V

VB 4 0 10V

E 5 0 3 2 200E3

RI 2 3 1G

R1 1 2 5k

R2 5 2 10k

R3 4 3 5k

R4 3 0 10k

.OP

.OPT nopage .TF V(5) VB .END

**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C

NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE

( 1) 3.0000  ( 2) 6.6666  ( 3) 6.6667  ( 4) 10.0000

( 5) 14.0000

VOLTAGE SOURCE CURRENTS

NAME CURRENT

VA   7.333E-04

VB  -6.667E-04

TOTAL POWER DISSIPATION 4.47E-03 WATTS

**** VOLTAGE-CONTROLLED VOLTAGE SOURCES

NAME      E

V-SOURCE1 1.400E+01

I-SOURCE -7.333E-04

**** SMALL-SIGNAL CHARACTERISTICS

V(5)/VB = 2.000E+00

INPUT RESISTANCE AT VB = 1.500E+04

OUTPUT RESISTANCE AT V(5) = 0.000E+00

Рис. 5.7. Выходной файл с результатами анализа схемы на рис. 5.6

Не забывайте, что PSpice не должен использоваться просто для получения численного результата. Надеемся, что после решения у вас возникнет много вопросов, анализ которых поможет вам больше узнать о работе исследуемых устройств.

При получении частотных характеристик ОУ следует использовать модель, учитывающую изменение его параметров при увеличении частоты. Для ОУ с типовыми характеристиками мы предлагаем модель, представленную на рис. 5.8. Исследуем модель, которая включает R_in=1 Мом; R₀=50 Ом; R_i1=1 кОм; С=15,92 мкФ и EG с коэффициентом усиления по напряжению A₀=100000. Последний параметр представляет собой низкочастотный коэффициент усиления или коэффициент усиления по постоянному току при разомкнутой обратной связи. При использовании этих значений, получим выходное напряжение на частоте f_c=10 Гц, при которой выходное напряжение снижается на 3 дБ.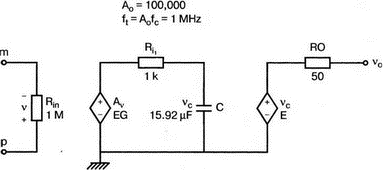

Рис. 5.8. Модель ОУ при частоте 10 Гц

Чтобы проверить расчет, нам необходимо получить коэффициент усиления при разомкнутой обратной связи. Это означает, что резистор обратной связи R₂ должен быть удален из схемы, но так как узел 5 должен иметь два элемента, связанных с ним, включим между узлом 5 и «землей» типовой резистор нагрузки R_L=22 кОм (см. рис. 5.9):

Op Amp Model with 3-Frequency at 10 Hz for Open-Loop Gain

VS 2 0 AC 1mV

EG 3 0 2 1 1E5

E 6 0 4 0 1

RI1 3 4 1k

RO 6 5 50

RI 0 1 10k

RL 5 0 22k

RIN 1 2 1MEG

N 40 15.92uF

.AC DEC 4 0 1 1MEG

.PROBE

.END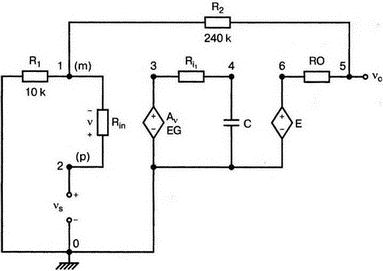

Рис. 5.9. Использование модели на рис. 5.8 для получения АЧХ усилителя с обратной связью 

Выполните моделирование и получите в Probe график частотной характеристики выходного напряжения V(5), показанный на рис. 5.10. Как и было предсказано, выходное напряжение падает от v₀=100 В при f=1 Гц до v₀=70 В при f=10 Гц, частоте, при которой коэффициент усиления падает на 3 дБ. Она представляется символом f_c. Выходное напряжение около 100 В соответствует коэффициенту усиления при разомкнутой обратной связи A₀=100000.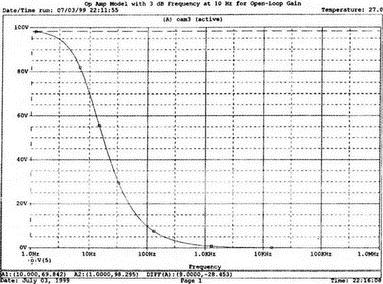

Рис. 5.10. АЧХ усилителя без обратной связи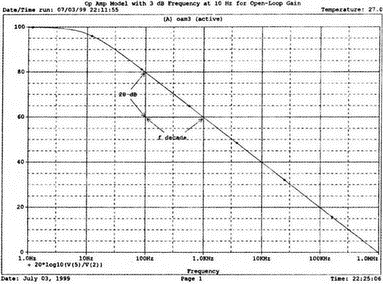

Рис. 5.11. Характеристика Боде для схемы на рис. 5.9 

Для анализа другой особенности модели ОУ, удалите график V(5) и постройте график зависимости

20·lg(V(5)/V(2)).

Из этого графика (рис. 5.11) ясно видно, что спад частотной характеристики составляет 20 дБ/дек. Возвратитесь входному файлу и добавьте следующую строку для введения в схему резистора R₂:

R2 5 1 240k

При этом получается практическая схема с выходным напряжением, ограниченным приемлемым значением. В Probe получается график v₀ со среднечастотным значением, близким к 25 мВ. Получите график Боде для отношения выходного напряжения к входному, как вы уже делали для схемы без обратной связи. Результаты показаны на рис. 5.12.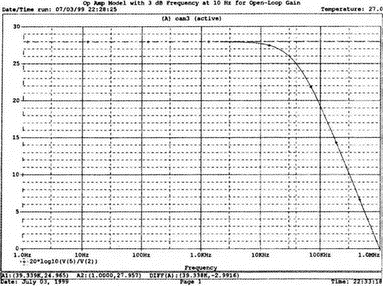

Рис. 5.12. График Боде для усилителя с обратной связью

Убедитесь, что коэффициент усиления на средних частотах равен А_mid=27,96 дБ и снижается на 3 дБ при f=39,3 кГц. Чтобы проверить правильность этих значений, вспомните, что коэффициент усиления равен единице при частоте f_t=A₀·f_c. В модели задано типичное значение частоты f_t=1 МГц. При этом также принимается, что f_с=10 Гц, что дает A₀=1Е5. Значение f_c установлено при R_i1=1 кОм и С=15,92 мкФ.

Обратите внимание, что ширина полосы частот при замкнутой обратной связи CLBW=f_tβ, а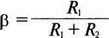

В нашем примере β=10/250=0,04 и f_tβ=40 кГц. Это приближенное значение находится в хорошем согласии с нашей моделью, которая дала f=39,33 кГц для частоты, при которой происходит снижение на 3 дБ. В качестве дальнейшего исследования модели измените значение резистора обратной связи на R₂=15 кОм, и снова проведите анализ. Убедитесь, что значение А_mid=7,959 дБ и f_3дБ=393,6 кГц. А какое значение для f_3дБ даст использование приближенной формулы и нового значения β?

Модель, которую мы использовали для ОУ в предыдущем примере, содержит достаточно много элементов, поэтому целесообразно оформить ее в виде подсхемы (subcircuit). При этом мы одновременно познакомимся с этим инструментом PSpice. Модель показана на рис. 5.13.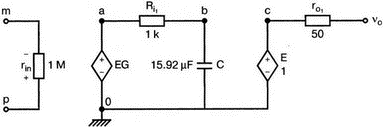

Рис. 5.13. Подсхема ОУ с обозначением узлов

Отметим, что узлы и элементы маркированы с использованием символов нижнего регистра. Это условие не обязательно, так как PSpice не учитывает регистра. То есть верхний и нижний регистры могут взаимозаменяться. Однако чтобы проще было идентифицировать подсхему и ее элементы, мы выбрали для меток узлов нижний регистр. Мы назначили номера и символы таким образом, чтобы не путать внутренние узлы подсхемы с внешними. Подсхема задается как независимая часть входного файла, но не является законченным входным файлом сама по себе. Команды описания подсхемы будут следующими: 

.subckt opamp m р v0

Eg а 0 р m 1e5

е c 0 b 0 1

rin m р 1meg

ri1 a b 1k

с b 0 15.92uf

ro1 с v0 5 0

.ends

Описание любой подсхемы начинается с команды .subckt. Первым элементом списка является имя подсхемы, которое в данном случае записано как opamp. Оно сопровождается набором узлов, которые связывают подсхему с остальной частью входного файла. Вы можете думать о них как об узлах, доступных для внешней части схемы. В данном примере — это узлы т, р и v₀. Опорный узел всегда обозначается как 0, и его не обязательно включать в перечень узлов.

Элементы в подсхеме задаются обычным способом. Так как подсхема не является законченным входным файлом, она может содержать «висящие» узлы. Команды ввода элементов выровнены для упрощения их идентификации, но это не обязательно. Команда .ends отмечает конец описания подсхемы.

Теперь мы готовы рассмотреть новую версию анализа ОУ с использованием подсхемы. Законченная схема показана на рис. 5.9 и повторена на рис. 5.14. После приобретения некоторого опыта вы, возможно, захотите рисовать подсхему в виде прямоугольника или треугольника. Как видно из рисунка, узлы m, р и v₀ имеют новые обозначения. Они получили метки 1, 2 и 3 соответственно. Чтобы использовать подсхему, основной входной файл должен содержать команду ввода подсхемы:

X 1 2 3 opam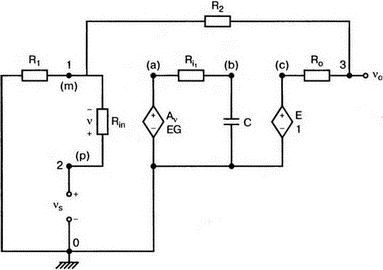

Рис. 5.14. Модель, показывающая подсхему в составе общей схемы для вызова 

Здесь X обозначает обращение к подсхеме. Узлы 1, 2 и 3 приводятся в порядке, соответствующем узлам m, p и v₀ в подсхеме. Это позволяет подсхеме получать обозначение узла, передаваемое от основного схемного файла. Инструкция также содержит имя подсхемы opamp. Теперь рассмотрим весь входной файл:

Op Amp Analysis Using Subcircuit

VS 2 0 AC 1mV

R1 1 0 10k

R2 3 1 240k

X 1 2 3 opamp

.AC DEC 40 100 1MEG

.PROBE

.subckt opamp m p v0

eg a 0 p m 1e5

e с 0 b 0 1

rin m p 1meg

ri1 a b 1k

с b 0 15.92uf

ro1 с v0 50

.ends

.END

Выполните анализ и убедитесь, что он дает тот же результат, что и предыдущий анализ, в котором подсхема не использовалась.

Дифференцирующая схема, построенная на базе идеального ОУ, показана на рис. 5.15, а. Поскольку инвертирующий вход заземлен, v_c=v. Легко показать, что при R=0,5 Ом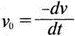

Таким образом, когда входное напряжение имеет форму треугольника, выходное напряжение должно быть прямоугольным (рис. 5.15, б). Используйте приведенный ниже входной файл, чтобы проверить этот вывод:

Differentiator Circuit v 1 0 PWL (0, 0 1s ,1V 2s,0)

С 1 2 2

R 2 3 0.5

X 2 0 3 iop

.subckt iop m р v0

ri m p 1meg

e v0 0 p m 2e5

.ends

.TRAN 0.05s 2s

.PROBE

.END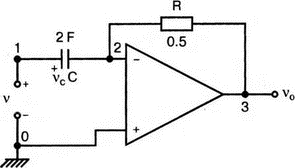

(a)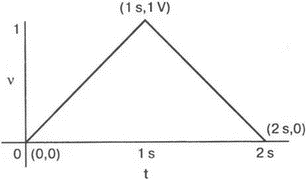

(b)

Рис. 5.15. Схема дифференциатора на базе ОУ

Выполните анализ и убедитесь, что выходное напряжение имеет прямоугольную форму с чередующейся полярностью и значениями напряжения от -1,0 В до +1 В. Эта инверсия происходит также и в ОУ. Постройте на одном графике временные зависимости для v(3) и v(1). Сравните ваши результаты с рис. 5.16. Обратите внимание, что команда входного файла для введения С не должна быть задана как

С 1 2 2F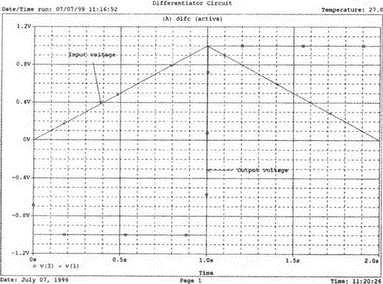

Рис. 5.16. График входного и выходного напряжений в схеме на рис. 5.15

В этом случае символ F будет восприниматься программой не как фарада, а как префикс и команда будет задавать значение 2 fF (фемтофарады). Если вы хотите, чтобы в записи всегда отражались единицы измерения, то вы можете использовать альтернативную форму записи:

С 1 2 2E6UF

Устройства, дуальные дифференцирующим схемам, называются интегрирующими схемами. На рис. 5.17, а резистор R и конденсатор С поменялись местами относительно рис. 5.15, а. Новая схема и есть интегратор (инвертирующий). Чтобы проверить его свойства, используйте входное напряжение (форма которого показана на рис. 5.17, б) и входной файл:

Integrator Circuit

v 1 0 PWL (0 0 0.01ms, -1V 1s, -1V 1000.01ms, 0V 2s,0V 2000.01ms, 1V

+ 3s, 1V)

R 1 2 0.5

С 2 3 2

X 2 0 3 iop

.subckt iop m p vo

ri m p 1meg

evo0pm2e5

.ends 

.tran 0.05s 3s

.probe

.end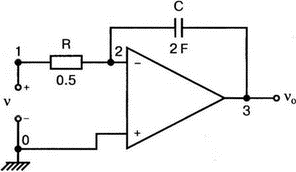

(a)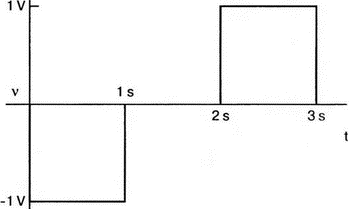

(b)

Рис. 5.17. Схема интегратора на базе ОУ

Обратите внимание, что «+» на строке 3 файла схемы указывает на продолжение команды, обычно длинной, которую необходимо перенести на следующую строку для удобства чтения. 

Выполните анализ и получите график v(1) вместе с графиком v(3). Убедитесь, что выходное напряжение начинается в момент фронта входного сигнала, линейно изменяется до максимального напряжения в 1 В, затем линейно спадает, достигая нуля между 2-й и 3-й с. Сравните ваши результаты с рис. 5.18.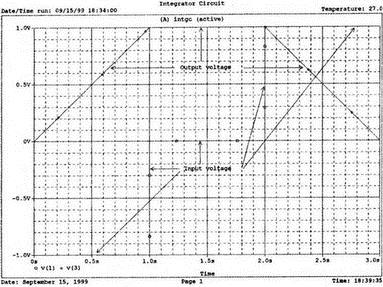

Рис. 5.18. График входного и выходного напряжений в схеме на рис. 5.17 

В качестве дополнительного упражнения, используйте входное напряжение такой же формы, как в задаче, посвященной дифференциатору, и найдите вид выходного напряжения. Проверьте, что этот график имеет форму параболы с установившимся значением -1 В, приведенную на рис. 5.19.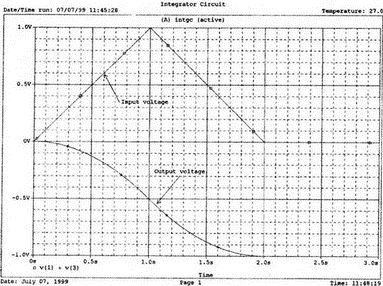

Рис. 5.19. График входного и выходного напряжений в схеме на рис. 5.17 при треугольной форме входного воздействия

Единичная ступенчатая функция показана на рис. 5.20, б. По определению она остается нулевой до t=0, а начиная с этого момента становится равной 1 В. Параметры элементов для схемы, показанной на рис. 5.20, a: R=2 Ом, R₁=1 Ом и С=0,125 Ф. Анализ схемы показывает, что

v₀(t) = (3 – 2e^-4t)u(t).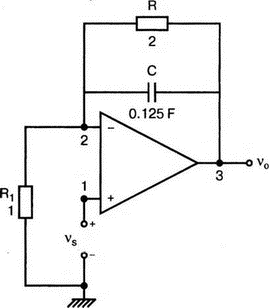

(а)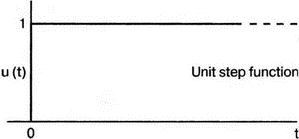

(b)

Рис. 5.20. Исследование реакции схемы с одним накопителем на ступенчатое воздействие: а) схема; б) временная зависимость входного воздействия

Перед началом анализа на PSpice полезно нарисовать график этой временной зависимости, чтобы представлять себе форму искомого напряжения. Входной файл:

Response to Unit Step Function

vs i 0 PWL (0,0 1us ,1V 5s, 1V)

С 2 3 0.125

R 2 3 2

R1 2 0 1

X 2 1 3 iop

.subckt iop m p v0

ri m p 1meg

e v0 0 p m 2e5

.ends

.TRAN 0.05s 3s

.PROBE

.END

После запуска анализа в программе Probe используем курсор, чтобы убедиться, что при t=0,5 с, V₀=2,73 В. Это соответствует значению, вычисленному из приведенного выше уравнения. Результаты анализа приведены на рис. 5.21.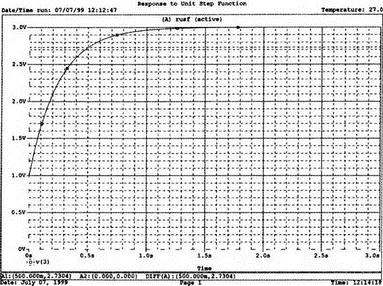

Рис. 5.21. Результат анализа схемы на рис. 5.20, а

Когда в схеме имеется несколько однотипных устройств, намного проще работать, представив их в виде подсхем. Предположим, что мы собираемся сравнить частотные характеристики для двух ОУ, схемы которых мы предварительно рассмотрели (в разделе «Амплитудно-частотные характеристики операционного усилителя»). Вспомним, что схемы были подобны за исключением того, что в первом случае R₂=240 Ом, а во втором случае R₂=15 Ом. Их частотные характеристики удобнее сравнивать на общем графике. 

Чтобы добиться этого, схему просто расширяют так, чтобы оба случая были исследованы одновременно. Мы определим ОУ подсхемой и используем рис. 5.22, чтобы обеспечить простую идентификацию узлов. Усилители Ор1 и Ор2 показаны просто в виде треугольников, поскольку вы уже знакомы с их моделью, нет необходимости повторять внутренние подробности. Теперь легко получить входной файл:

Double Op Amp Circuit for Gain-Bandwidth Analysis

VS1 2 0 AC 1raV

R1 1 0 10k

R2 3 1 240k

X1 1 2 3 opamp

VS2 5 0 AC 1mV

R3 4 0 10k

R4 6 4 15k

X2 4 5 6 OPAMP

.AC DEC 40 100 10MEG

.PROBE

.subckt opamp m p vo

eg a 0 p m 1e5

e с 0 b 0 1

rin m p 1meg

ri1 a b 1k

с b 0 15.92uf

ro1 с vo 50

.ends

.END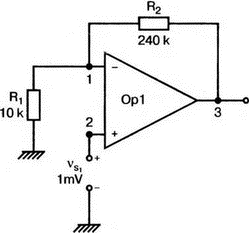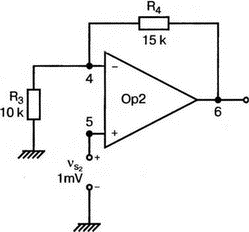

Рис. 5.22. Схема с двумя ОУ

Подсхема описывается так же, как и прежде. После создания подсхемы вы можете просто скопировать ее в любой входной файл, где она необходима. В данном случае она вызывается дважды — сначала командой X1, а затем командой X2. Список узлов, используемых в каждом случае, такой же, как на рис. 5.22.

Выполните анализ и затем получите графики

20·lg(V(3)/V(2)),

и

20·lg(V(6)/V(5)).

Используйте режим курсора, чтобы найти отметку 3 дБ для первого графика. Обратите внимание, что при включении режима курсора автоматически выбирается первый график. Убедитесь, что А_mid=27,96 дБ и f_3дБ=39,4 кГц.

Исследуйте теперь второй график. Нажмите Ctrl и → (стрелку вправо), чтобы перевести курсор на второй график. Затем двигайтесь по второму графику, пока не достигнете нужной точки. Обратите внимание, что второй график показывает А_mid=7,96 дБ, что на 20 дБ меньше, чем у первого. Искомая частота будет соответствовать коэффициенту усиления 4,96 дБ (7,96–3,00). Убедитесь, что это дает f_3дБ=394 кГц. Эти результаты соответствуют полученным в предыдущих примерах. Сравните полученный вами двойной график с рис. 5.23.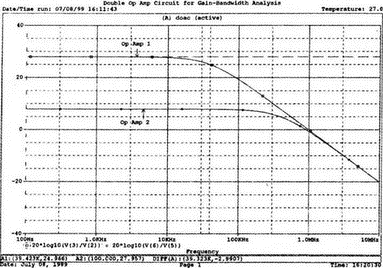

Рис. 5.23. Результат анализа схемы с двумя ОУ

Для получения более крутых границ полосы пропускания, чем у простых однополюсных фильтров, содержащих, например, только один конденсатор, могут применяться высокочастотные, низкочастотные и полосовые активные фильтры. Классическим примером таких устройств являются фильтры Баттерворта. 

ОУ часто используются при разработке активных фильтров, поскольку получить усилители с высокими добротностями на базе ОУ достаточно просто. Мы не будем касаться теории фильтров в нашем обсуждении. Если вы изучаете активные фильтры впервые, обратитесь к другим источникам, чтобы лучше оценить элегантность и простоту этих схем.

Воспользуемся таблицами нормированных многочленов Баттерворта, чтобы найти коэффициенты для фильтра второго порядка:

s² + 1,414s + 1.

Фильтр второго порядка показан на рис. 5.24. Для вводного примера найдем элементы R₁, R₂, R и С для фильтра Баттерворта с частотой среза f_c=5 кГц. Как обычно, в качестве частоты среза принимается частота, при которой характеристика снижается на 3 дБ. Согласно теории, низкочастотный коэффициент усиления задается выражением: 

A_vo = 3 – 2k,

где k представляет собой коэффициент затухания, определенный как половина коэффициента при s² из таблицы полиномов Баттерворта (см. Hillburn and Johnson. Manual of Active Filter Designs, McGraw-Hill, 1973). Для этого примера k=0,707 и

A_v0 = 3 - 1,414 = 1,586.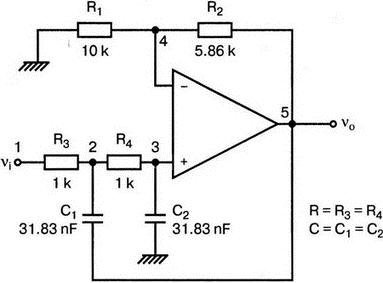

Рис. 5.24. Низкочастотный фильтр Баттерворта второго порядка 

Допустим, что R₁=10 кОм. Из выражения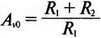

получаем R₂=5,86 кОм. Если положить R=1 кОм, из выражения f_c=1/(2πRC) найдем С=31,83 нФ. Чтобы проверить теорию Баттерворта, используем идеальную модель ОУ в качестве подсхемы, как показано на рис. 5.25. Для этого создайте следующий входной файл:

Second-Order Butterworth Filter

V1 1 0 AC 1mV

R3 1 2 1k

R4 2 3 1k

R1 4 0 10k

R2 5 4 5.86k

C1 2 5 31.83nF

C2 3 0 31.83nF

X 4 3 5 iop

.AC DEC 40 1 100kHz

.PROBE

.subckt iop m p vo

e vo 0 p m 2e5

rin m p 1meg

.ends

.END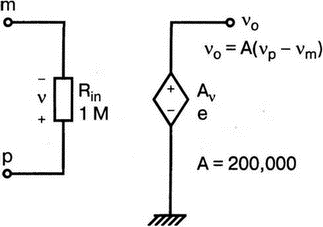

Рис. 5.25. Подсхема для идеального ОУ

Проведите анализ и получите график V(5)V(1). Выясните, что А_v0=1,586, что соответствует нашему расчету. Затем удалите этот график и получите график зависимости

20·lg(V(5)/(V(1)·1,587В)).

Убедитесь, что f_c=5 кГц. Этот фильтр второго порядка должен иметь вдвое большую крутизну спада, чем фильтр первого порядка. Вспомним, что фильтр первого порядка имеет скорость спада 20 дБ/дек. Убедитесь, что при f=10 кГц A_v=12,31 дБ, а при f=100 кГц A_v=52,05 дБ, что составляет приблизительно 40 дБ/дек. Этот график показан на рис. 5.26.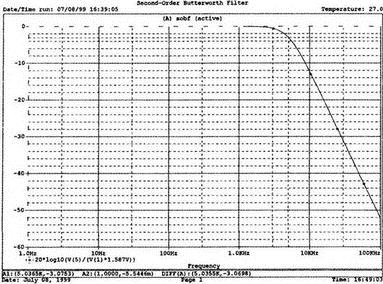

Рис. 5.26. График Боде для низкочастотного фильтра Баттерворта второго порядка

В качестве другого примера рассмотрим фильтр Баттерворта четвертого порядка, предназначенный для работы на частоте f_c=1 кГц. Из таблицы полиномов находим коэффициенты:

(s² + 0,765s + 1)·(s² + 1,848s + 1).

Коэффициент затухания k равен половине коэффициента при s в каждом квадратном уравнении, давая k₁=0,383 и k₂=0,924:

A_v1 = 3 – 2k₁ = 3 – 0,765 = 2,235 и A_v2 = 3 – 2k₂ = 1,152.

Для первого каскада примем R₁=10 кОм и с помощью уравнения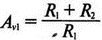

найдем R₂=12,35 кОм. Приняв для второго каскада R₁=10 кОм, получим R₂=1,52 кОм. При f_c=1 кГц, если положить R=1 кОм, С=0,16 мкФ. Схема показана на рис. 5.27. Поскольку каждый элемент должен иметь уникальное обозначение, вычисленные здесь значения R и С относятся к соответствующим резисторам и конденсаторам каждого из каскадов. Входной файл при этом:

Fourth-Order Butterworth Filter

V1 1 0 AC 1mV

R3 1 2 1k

R4 2 3 1k

R1 4 0 10k

R2 5 4 12.35k

R7 5 6 1k

R8 6 7 1k

R5 8 0 10k

R6 9 8 1.52k

C1 2 5 0.16uF

C2 3 0 0.16uF

C3 6 9 0.16uF

C4 7 0 0.16uF

.AC DEC 40 1 10kHz

.PROBE

.subckt iop m p vo

E vc N

i p m 2e5

rin m p 1meg

.ends

X1 4 3 5 iop

X2 8 7 9 iop

.END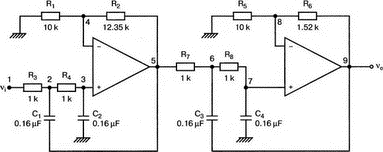

Рис. 5.27. Полосовой фильтр Баттерворта четвертого порядка

Выполните анализ и затем получите совместный график для V(5)/V(1), (V)9/V(5), и V(9)/V(1). Они представляют собой коэффициенты усиления первого и второго каскадов и полный коэффициент усиления соответственно. Так как они выражены не в децибелах, вы легко сможете проверить, что A_v1=2,235, A_v2=1,152, а общий коэффициент усиления A_v=A_v1·A_v2=2,575. Вы можете найти эти значения, используя режим курсора при низких частотах. Нажимайте Ctrl и →, чтобы выбрать нужный график. Сравните полученные вами графики с представленными на рис. 5.28.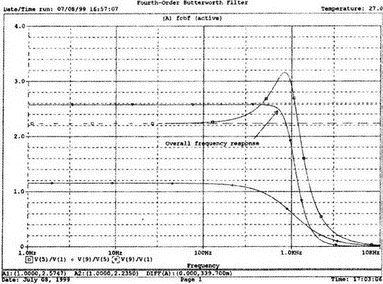

Рис. 5.28. АЧХ фильтра Баттерворта четвертого порядка

Получите распечатку результатов анализа, включая все три графика для дальнейшего изучения. Обратите внимание на интересный пик на графике A_v1. Он компенсируется провалом на графике А_v2, поэтому график полного коэффициента усиления становится плоским почти на всей полосе пропускания, круто падая при частоте, близкой к 1 кГц.

Крутизну легче определить из графика в децибелах. Используйте характеристику 20·lg(V(9)/V(1)) и так далее, заменив три графика логарифмическими характеристиками. Убедитесь, что для полной схемы, f_c=1 кГц. Также пронаблюдайте скорость спада для каждого из трех графиков. Вы сможете показать, что для каждого из двух каскадов, крутизна спада составляет приблизительно 10 дБ/дек по сравнению с приблизительно с 20 дБ/дек для общей характеристики. Разве не вызывает восхищения простота восприятия основных идей при передаче их графическим способом. Вы должны также оценить, сколько времени и усилий сэкономлено при использовании такого мощного вычислительного инструмента, как PSpice. Сравните кривые представленные на рис. 5.29, с полученными графиками.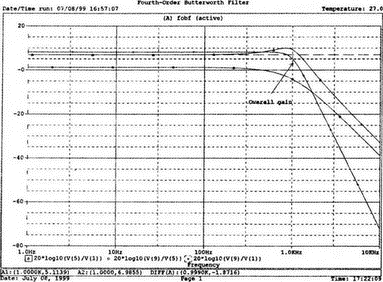

Рис. 5.29. Логарифмические АЧХ (ЛАЧХ) фильтра Баттерворта четвертого порядка

Мы можем показать одно дополнительное свойство фильтра Баттерворта, слегка модифицировав предыдущий входной файл. Сравните фильтры второго и четвертого порядков. Будут необходимы некоторые вычисления, поскольку мы не имеем данных для двухкаскадного фильтра при f=1 кГц.

Низкочастотный коэффициент усиления будет таким же, как вычисленный ранее для фильтра второго порядка, а именно: A_v=1,586. Положив R₁=10 кОм, получим R₂=5,86 кОм.

При R=1 кОм найдем, что С=0,159 мкФ. Дополнение к схеме на рис. 5.27, позволяющее включить в схему фильтр второго порядка, показано на рис. 5.30. Отметим, что это дополнение имеет номера узлов большие, чем приведенные на рис. 5.27. Этот фильтр имеет собственный вход и физически не связан с четырехкаскадным фильтром. Если дополнить входной файл соответствующей информацией, он примет вид:

Fourth-Order Butterworth Filter Compared with Second-Order

VI 1 0 AC 1mv

R3 1 2 1k

R4 2 3 1k

R1 4 0 10k

R2 5 4 12.35k

R7 5 6 1k

R8 6 7 1k

R5 8 0 10k

R6 9 8 1.52k

C1 2 5 0.16uF

C2 3 0 0.16uF

C3 6 9 0.16uF

C4 7 0 0.16uF

VII 10 1 AC imV

R9 13 0 10k

R10 14 13 5.36k

R11 10 11 1k

R12 11 12 1k

C5 11 14 0.159uF

C6 12 0 0.159uF

X1 4 3 5 iop

X2 8 7 9 iop

X3 13 12 14 iop

.AC DEC 40 1 10kHz

.PROBE

.subckt iop m p vc

VC 0pm 2e5

ein m p 1meg

.ends

.END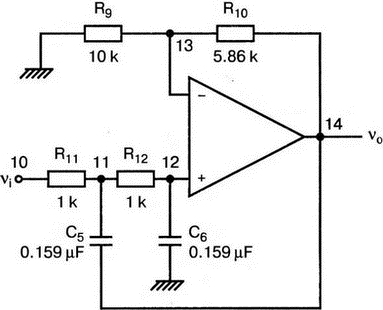

Рис. 5.30. Дополнение к схеме на рис. 5.27, позволяющее включить в схему фильтр второго порядка

Выполните анализ и получите графики в децибелах V(9)/V(1) для фильтра четвертого порядка и V(14)/V(10) для фильтра второго порядка. Вы должны получить A_v=4,006 дБ (второй порядок) и A_v=8,214 дБ (четвертый порядок). Мы хотим показать их при сравнимой базе, поэтому построим графики

20·lg(V(14)/V(10)),

и

20·lg(V(9)/V(1)) – 4,208.

Значение 4,208 представляет смещение второго графика относительно первого, нормализующего второй график относительно первого. Эти графики (рис. 5.31) с накладывающимися в низкочастотном диапазоне траекториями ясно показывают, что оба фильтра Баттерворта имеют одинаковую частоту f_c=1 кГц. Это относится к фильтрам Баттерворта всех порядков.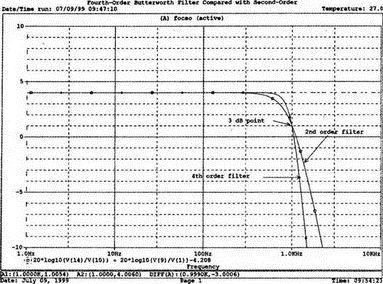

Рис. 5.31. Логарифмических АЧХ для фильтров Баттерворта второго и четвертого порядков

В простой резонансной схеме резонансные свойства RLC-цепи используются для создания крутого спада характеристики на границах полосы пропускания. На рис. 5.32 показан входной колебательный контур, содержащий V_s, R, L и C. Выберем параметры элементов, обеспечивающие необходимую ширину полосы частот В и добротность Q.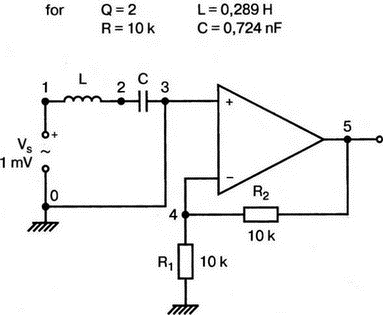

Рис. 5.32. Активный резонансный полосовой фильтр с добротностью Q = 2

Центральная частота принимается равной частоте резонанса LС-контура: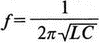

Добротность Q определяется по формуле Q=ω₀L/R. В таком фильтре В=f₀/Q=R/2πL. Например, выберем добротность Q=2, f₀=11 кГц и R=10 кОм. При этом L=0,289 Гн и С=0,724 нФ. В завершение выберем R₁=10 кОм, чтобы обеспечить необходимое значение A_v этого неинвертирующего усилителя. Входной файл:

Active Resonant Band-Pass Filter

vs1 о AC 1mv

R 3 0 10k

R1 4 0 10k

R2 5 4 10k

L 1 2 0.289H

С 2 3 0.724nF

X 4 3 5 iop

.AC DEC 40 1kHz 100kHz

.PROBE

.subckt iop m p vo

e vo 0 p m 2e5

rin m p 1meg

.ends

.END

Проведите анализ и получите график отношения выходного напряжения к входному (V(5)/V(1)) в логарифмическом масштабе. Проверьте центральную частоту и ширину полосы частот. Значения частот спада на 3 дБ составляют f=8,6 кГц и f=14,1 кГц, что обеспечивает полосу пропускания В=5,5 кГц. При этом центральная частота оказывается равной приблизительно 11,2 кГц.  

Получим также график VP(5), чтобы наблюдать, как фазовый угол изменяется вблизи резонансной частоты. Он равен нулю при f=11 кГц. Интересно сравнить две схемы этого типа, которые имеют различные значения добротности. Мы получили результаты при добротности Q=2, а теперь исследуем другую схему при Q=5. На рис. 5.33 показана соответствующая схема. Ширина полосы частот В=2,2 кГц, и сохраняя значение R=10 кОм, получим L=0,723 Гн и С=0,289 нФ.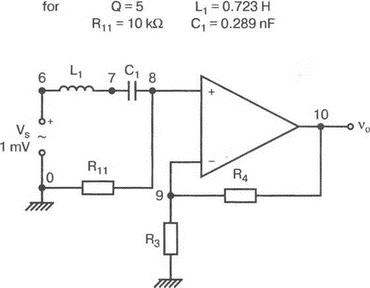

Рис. 5.33. Схема дополнения, позволяющая исследовать полосовой фильтр с добротностью Q = 5

Узлы пронумерованы таким образом, чтобы схемой можно было дополнить первоначальный входной файл. Это позволит нам получить АЧХ для обеих схем на одном графике. Добавьте следующие команды к предыдущему входному файлу:

VS1 6 0 AC 1mV

R11 8 0 10k

R3 9 0 10k

R4 10 9 10k

L1 6 7 0.723Н

C1 7 8 0.289nF

X1 9 8 10 iop

Выполните анализ и получите в одном окне графики

20·lg(V(5)/V(1)),

и

20·lg(V(10)/V(6)).

Посмотрите влияние добротности на форму графиков при Q=5 и Q=2. С помощью курсора проверьте ширину полосы частот при Q=5. Она должна быть почти точно В=2,2 кГц. Эти кривые показаны на рис. 5.34.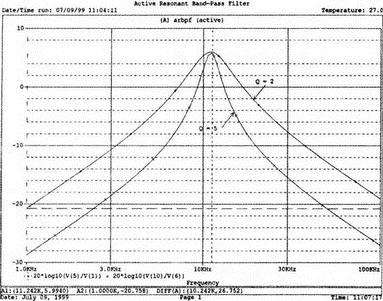

Рис. 5.34. Графики Боде для сравнения АЧХ при добротностях Q = 2 и Q = 5 

Получите другой график, используя VP(5) для одной кривой и VP(10) для другой. Это покажет сравнение сдвигов фазы для двух случаев. Сравните результат с полученным на рис. 5.35.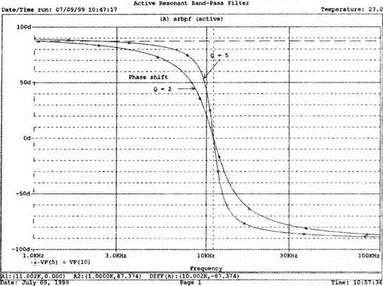

Рис. 5.35. Графики Боде для сравнения фазочастотных характеристик при добротностях Q = 2 и Q = 5

Использование катушки индуктивности в полосовом фильтре не всегда желательно, тем более что в некоторых случаях значение индуктивности очень велико. На рис. 5.36 представлена схема, в которой для обеспечения заданной полосы пропускания используются только конденсаторы и резисторы.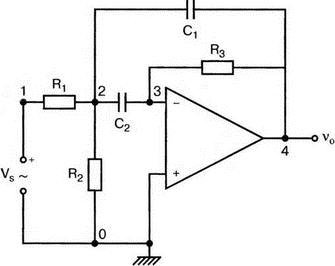

Рис. 5.36. Активный полосовой RC-фильтр

Для определения параметров элементов можно использовать следующие формулы: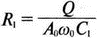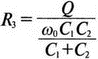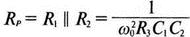

Для примера мы выберем A₀=50, f₀=160 Гц и В=16 Гц. Для удобства примем С₁=С₂=0,1 мкФ. Выражение для добротности Q=f₀/B. Теперь найдите R₁, R₂ и R₃. Сравните ваши ответы с приведенными в последующих результатах анализа на PSpice. Обратите внимание, что значения сопротивления были немного округлены. Входной файл:

Active RC Band-Pass Filter

VS1 6 0 an 1mv

R1 1 2 2k

R2 2 0 667

R3 4 3 200k

C1 2 4 0.1uF

C2 2 3 0.1uF

X 3 0 4 iop

.AC DEC 100 1 1Mz

.PROBE

.subckt iop m p vo

e vo 0 p m 2e5

rin m p 1meg

.ends

Проведите анализ и получите график V(4)/V(1), показывающий А₀=50 при f₀=158 Гц. Удалите этот график и постройте новый в логарифмическом масштабе, чтобы найти полосу пропускания. Убедитесь, что f₁=151 Гц и f₂=167 Гц, что дает B=16 Гц. На рис. 5.37 показан результат с курсором в одной из точек, соответствующих снижению на 3 дБ.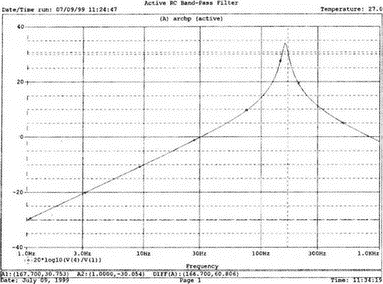

Рис. 5.37. Характеристика Боде для схемы на рис. 5.36

Х[name] [<node>]* <sname>

Например, запись

XI 9 8 10 iop

указывает, что подсхема подключена в узлах 9, 8 и 10 к основной схеме. Имя подсхемы — iop. Входной файл содержит описание подсхемы. Он мог бы иметь, например, такой вид:

.subckt iop 1 2 3

…

…

.ends

где запись iop идентифицирует подсхему, в которой узлы подсхемы 1, 2 и 3 подключаются к внешним узлам 8, 9 и 10 соответственно команде X. Строка .ends показывает конец описания подсхемы. 

Использование подсхем наиболее удобно, когда во входном файле необходимо использовать устройство, модель или группу элементов более одного раза. Например, все команды X1, Х2 и Х3 могли бы обращаться к одному и тому же устройству: iop.

5.1. Идеальный инвертирующий ОУ, показанный на рис. 5.2, имеет следующие параметры элементов: R₁=2 кОм; R₂=15 кОм; А=100000 и R_i=1 Мом. Проведите PSpice анализ, чтобы определить коэффициент усиления по напряжению, входное и выходное сопротивления. Значение 1 МОм для встречается на практике. Какие различия в результатах вы получите, если выполнить анализ на PSpice для R_i=1 ГОм?

5.2. Рассчитайте идеальный неинвертирующий ОУ, показанный на рис. 5.3, таким образом, чтобы иметь коэффициент усиления по напряжению, равный 20. Выберите значения для R₁ и R₂, и выполните PSpice анализ, чтобы проверить ваш расчет. 

5.3. Идеальный ОУ, показанный на рис. 5.5, должен использоваться при значениях входных сигналов v_a=3 В и v_b=10 В. При R₁=5 кОм, R₂=10 кОм, R₃=10 кОм и R₄=5 кОм, найдите выходное напряжение, используя PSpice. Сравните результаты с теми, что получили в примере из текста при R₁=R₃ и R₂=R₄. Определите роль R₃ и в определении коэффициента усиления по напряжению.

5.4. Для модели ОУ, приведенной на рис. 5.8, f_t=1 МГц и f_c=10 Гц. Пересмотрите модель, чтобы учесть f_t=2 МГц и f_c=10 Гц. Используйте R₁=10 кОм и R₂=240 кОм. Найдите коэффициент усиления на средних частотах и верхнее значение частоты для снижения на 3 дБ. Сравните ваши результаты с приведенными в текстовом примере.

5.5. На рис. 5.15 произведение RC составляет 1 с. Покажите, что использование чаще применяемых на практике значений С=50 мкФ и R=20 кОм в том же входном файле должно привести к тем же результатам, что и в текстовом примере. Затем при использовании С=50 мкФ и R=10 кОм выполните анализ снова. Объясните различие между этим и предыдущим результатами.

5.6. Используя схему на рис. 5.17 при С=50 мкФ и R=20 кОм, выполните на PSpice анализ с тем же входным сигналом, что и на рисунке. Сравните полученные результаты с рис. 5.18. Затем при использовании С=50 мкФ и R=10 кОм выполните анализ снова. Объясните различие между этим и предыдущим результатами.

5.7. На рис. 5.38 показан ОУ первого порядка, у которого

v_s = 4 – 4u(t) В,

где u(t) представляет собой единичную ступенчатую функцию. Анализ показывает, что

v_c(t) = 10e^-4t В и

v₀(t) = -v_c(t) В.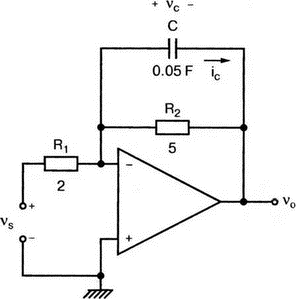

Рис. 5.38.

Для t≥0 выполните PSpice анализ, чтобы проверить предсказанные результаты.

5.8. На рис. 5.39 приведена схема с ОУ, для которой

v_s(t) = 3 - 3u(t) В.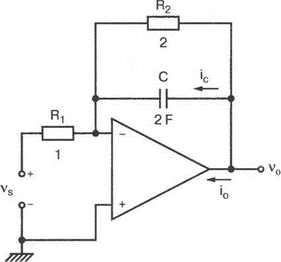

Рис. 5.39

Найдите v₀(0), i_с(0), i₀(0) и получите график v₀(t), используя PSpice.

5.9. Рассчитайте фильтр низкой частоты первого порядка, показанный на рис. 5.40, с частотой среза f₀=5 кГц. Используйте R=R₁=1 кОм и рассчитайте С. Найдите коэффициент усиления на средних частотах и используйте программу Probe для проверки расчета.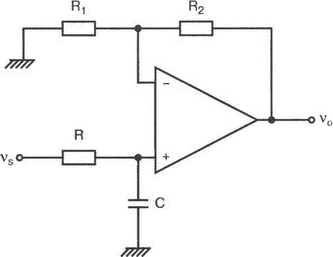

Рис. 5.40.