• Главная
• В избранное
• Наш E-MAIL
• Добавить материал
• Нашёл ошибку
• Вниз

В Доме ребенка плоские вкладыши, которые развивают сенсорику, познакомили детей со многими геометрическими фигурами: квадрат, прямоугольник, треугольник, многоугольник, круг, овал и т. д. Благодаря прилагающимся карточкам малыши научились узнавать геометрические фигуры по нарисованным очертаниям. Кроме того, у нас есть металлические вкладыши, воспроизводящие уже известные детям геометрические фигуры. Их можно обводить, полученные контуры затем заштриховывать цветными карандашами (упражнение учит владеть пишущими инструментами).

Геометрический материал начальной школы можно рассматривать как продолжение знакомых упражнений. Он напоминает металлические вкладыши. Но каждая рамка прикреплена к квадратной дощечке-основе. Теперь не нужны ни специальные пюпитры, ни рамы, как для остальных вкладышей. Каждая фигура является завершенной и независимой. Дощечка белая, контур зеленый, а сам вкладыш, подвижная часть, красный. Когда вкладыш лежит на своем месте, то получается красная фигура в зеленой рамке. Подвижные вкладыши сделаны не из одного, а из многих частей, закрепленных на белом пространстве дощечки. Основное назначение этого материала — позволить ребенку самостоятельно упражняться в геометрии, научиться решать разные задачи. Возможность манипулировать геометрическими фигурами, располагать их по-разному, исследовать их различия чрезвычайно привлекает детей. Наши материалы напоминают игры на терпение, придуманные для малышей, только с более определенной образовательной целью. Ребенок уясняет основные геометрические принципы, чего так трудно достичь традиционными методами обучения. Понимание разницы между фигурами равными, подобными или равными по площади, понимание сути преобразования фигур, теоремы Пифагора возникает спонтанно и приносит ученикам много радости. Ребенок учится выполнять действия с дробями, упражняясь с цилиндрическими вкладышами. Осознание значения дроби, преобразование обычной дроби в десятичную, становится новым интеллектуальным достижением ученика, показателем и высокого уровня знаний, и развития умственных способностей. В обычной школе даже старшеклассник порой еще так не чувствует соотношения геометрических фигур, как наши малыши, совершившие все эти открытия самостоятельно, с удовольствием и неослабевающим энтузиазмом. Они свободно и стремительно движутся своим путем, не истощая, а накапливая внутреннюю энергию, в то время как остальные школьники напоминают усталых странников, бредущих босиком по острым камням.

Мы предоставляем ученику возможность свободно упражняться в тот момент, когда он наиболее готов к этому, и заниматься столько, сколько ему нужно, чтобы идея созрела в его сознании. В конце концов, у ребенка развивается абстрактное мышление. В основе этого достижения — интеллектуальная зрелость и достаточные знания, две опоры для человека, идущего к вершине. Мы столкнемся с этим феноменом не раз. Каждый шаг на пути внутреннего созревания, каждое новое обретенное знание становится для ученика площадкой для следующего взлета. Интеллект, чтобы подняться к абстракции, нуждается в опоре, как самолет во взлетной полосе. Нужен разбег, время, необходимое для разгона. Нужно крепкое оснащение, подготовка — одного желания мало. Самолет без топлива, птица без сильных крыльев — разве взлетят они? То же самое происходит с детским интеллектом. Пусть человек от природы наделен высокими способностями, ему нужно опираться на реальный опыт и пополнять запасы внутренней энергии. Чем больше материал привлекает внимание ученика, тем больше он дает возможностей для абстрагирования, для развития творческого воображения (следствия растущего внутреннего потенциала).

Геометрические вкладыши во многом удовлетворяют интеллектуальные потребности детей. С ними можно упражняться не только в составлении фигур, в сравнении их, но также в рисовании. Долгое, тщательное срисовывание позволяют ребенку сосредоточиться на каждой детали, обдумать каждую мелочь. Причем рисунок, как станет видно позднее, может быть двух видов: геометрический и художественный, возможно и смешение жанров. Геометрический рисунок воспроизводит фигуры. Выполняя его, малыш учится владеть различными инструментами, линейкой, угольником, циркулем, транспортиром. Благодаря геометрическому рисованию, достигается истинное понимание геометрии, чему способствует специальный альбом, также входящий в комплект.

Художественное рисование состоит в комбинировании различных фигур (из комплекта вкладышей) и рисовании их цветными карандашами, красками. Это уже настоящее творчество. Наши вкладыши так пропорциональны, их сочетания так гармоничны, что способствуют развитию эстетического вкуса ребенка. Мы можем копировать композиции великих мастеров, таких как Джотто.

Соединение художественного и геометрического рисования начинается с украшения различных частей фигуры (центра, угла, противоположных сторон), а затем можно несколькими деталями, нарисованными от руки, завершить рисунок, превратив его из чертежа в художественную композицию.

 Первая серия вкладышей: квадраты, фигуры, состоящие из отдельных частей.

Эта серия состоит из 9 квадратных вкладышей, в основе которых есть углубления — одинаковые белые квадраты со стороной 10 см. В одно углубление вложен целый квадрат, в другие — те же квадраты, но состоящие из отдельных частей:

– квадрат, состоящий из 2 равных прямоугольников;

– квадрат, состоящий из 4 равных прямоугольников;

– квадрат, состоящий из 8 равных прямоугольников;

– квадрат, состоящий из 16 равных прямоугольников;

– квадрат, состоящий из 2 равных треугольников;

– квадрат, состоящий из 4 равных треугольников;

– квадрат, состоящий из 8 равных треугольников;

– квадрат, состоящий из 16 равных треугольников.

Ребенок может взять квадрат, состоящий из 2 равных прямоугольников, и квадрат, состоящий из 2 равных треугольников, поменять местами части фигур, то есть первый квадрат заполнить двумя треугольниками, а второй — прямоугольниками. Части фигур можно наложить друг на друга внутренней стороной (на внешней будут мешать кнопки, которые нужны для удобства доставания фигуры из рамки). Наложение позволяет установить равенство фигур. Однако треугольник и прямоугольник — разные по форме фигуры, хотя каждая из них составляет ровно половину того же самого квадрата. Так рождается ощущение равенства площади фигур. Два треугольника равны между собой, и два прямоугольника равны между собой. Ученик сравнивает их, накладывая фигуры друг на друга, и замечает, что часть треугольника, выходящая за пределы прямоугольника, равна той части треугольника, которая прикрыта прямоугольником. Следовательно, треугольник и прямоугольник отличаются по форме, но равны по площади.

Аналогичные наблюдения повторяются и с другими квадратами, разделенными на большее количество частей. Квадратики, являющиеся четвертой частью большого квадрата (они получились в результате деления фигуры по медианам), равны между собой и равны по площади треугольникам, возникшим в результате деления большого квадрата по диагоналям. Фигуры, одинаковые по форме, но отличающиеся по размеру, являются подобными. Прямоугольник — половина большого квадрата, подобен прямоугольнику, являющемуся ¹/₈ большого квадрата, при этом они не равны между собой, у них разная площадь. Также подобны друг другу большой квадрат и маленький, четвертушка большого. И т. д.

В разделении квадрата на части уже содержится идея дроби, хотя это пока еще не тот материал, который специально предназначен для изучения дробей.

 Вторая серия вкладышей: дроби.

Десять дощечек с углублениями в форме круга диаметром 10 см, белого цвета. В первое углубление вложен целый круг, в остальные — такие же круги, но поделенные на 2, 3, 4, 5, 6, 7, 8, 9, 10 равных частей. Дети учатся измерять углы каждой части. Для этого мы вырезали картонный круг. Центр обозначен черной точкой на светлом фоне. Очерчен полукруг, радиус которого равен радиусу вкладышей. Этот полукруг поделен лучами на 18 секторов. Лучи выходят за пределы дуги полукруга, сверху написаны числа: 0, 10, 20 — и так до 180. Дуга каждого сектора поделена еще десятью маленькими делениями. Получилась шкала, где одно деление равно одному градусу. Линии, соединяющие 0 и 180 и идущие от центра к 90°, проведены толще, чем остальные, они чуть выпуклые, что позволяет накладывать фигуры точнее. Ученик кладет фигуру вкладыша на картонный расчерченный круг так, что вершина угла совпадает с центром, а одна из сторон заканчивается на нуле. Читаем цифру над окончанием другой стороны фигуры — это и есть величина угла в градусах. После таких упражнений, после работы с транспортиром, ребенок умеет измерять любые углы. Он знает, что круг — это 360°, полукруг — 180°, а прямой угол — 90°.

Теперь можно сосчитать, сколько градусов составляет угол седьмой части круга. 360°: 7=51°, это легко проверить наложением фигуры на расчерченный круг. Подсчеты и измерения можно повторить со всеми вкладышами, составляющими от половины до десятой части круга.

¹/₃ круга = 120°, 360°: 3-120°,

¹/₄ круга = 90°, 360°: 4 = 90°, и т. д…

¹/₁₀ круга = 36°, 360°: 10 = 36°.

Если знаменатели равны, то сложение дробей происходит путем простого сложения числителей. Знаменатель сохраняется.

Ребенок запоминает дроби: ¹/₂, ¹/₃, ... ¹/₁₀ У него есть и материальной восприятие, и арифметическое вычисление. С этим материалом можно совершать бесчисленные упражнения, осваивая счет с дробями. К примеру, ученик берет круг, состоящий из двух частей, и заполняет его фигурами — четвертинками круга. Он может оставить одну половину, а вместо второй положить две четвертинки. Вскоре он поймет: ¹/₂+¹/₂=¹/₄+¹/₄ +¹/₄+¹/₄, а две половинки равны четырем четвертям: ²/₂ = ⁴/ _⁴. Ребенок мысленно считает дроби, видя части круга, и в состоянии выразить свое понимание при помощи математической записи. Наблюдения можно анализировать более глубоко.

¹/₂+¹/₂=²/₂

¹/₄+¹/₄ +¹/₄+¹/₄=⁴/₄

¹/₂+¹/₂=¹/₄+¹/₄ +¹/₄+¹/₄

Две половины и четыре четверти — это целый круг. Заполняя круг разными по размеру частями (например, один полукруг и две четверти), ребенок видит соотношение дробных чисел.

1 = ¹/₂+²/₄, то есть ¹/₂=²/₄. То же и с остальными дробями.

Ребенок учится сокращать дроби, видеть их простейшее выражение. Приходит очередь и сложных примеров, которые сначала выполняются при помощи вкладышей, а затем только на бумаге.

Теперь можно переходить и на другие предметы, поддающиеся счету и делению, в частности, на бусины, жетоны, фасолины.

Мы составляем приказания:

– Возьми ¹/₅ от 25 бусин.

– Возьми ¹/₄ от 36 жетонов.

– Возьми ¹/₃ от 27 фасолин.

Бывают приказания, требующие вычислений в два действия, к тому же разными способами:

– Возьми ²/₅ от 60 бусин. 60: 5 = 12; 2x12 = 24 или 2x60 = 120;

120: 5 = 24 и т. д.

Преобразование обычных дробей в десятичные: дощечка, напоминающая круглые вкладыши, только фон не светлый, а темный, на нем обозначены деления.

Штрихи подлиннее делят круг на 10 частей, они обозначены цифрами: 0, 10… 90. Штрихи покороче делят каждую дугу пополам, еще более короткие делят каждую половину на пять частей. Получается круг, поделенный на 100 частей. Линия от центра к вершине, над которой стоит 0, (радиус) выпуклая, чтобы точнее расположить фигуры, которые мы хотим измерить.

Чтобы перевести обычную дробь в десятичную, мы берем часть вкладыша, уже измеренную, располагаем ее в нашем круге, совмещая центры и одну из сторон фигуры с выпуклым радиусом. Остальная часть фигуры должна лежать справа от радиуса, в сторону увеличения цифр. Если мы положим так одну четвертую часть круга, то сразу увидим по цифре над окончанием второй стороны фигуры, что ¹/₄ — 0, 25.

Можно положить рядом, сторона к стороне, несколько фигур-вкладышей и увидеть:

¹/₃+¹/₄+¹/₈⁼ 0,70 (примерно).

Этот материал прекрасно развивает арифметические навыки. Круг (единичное целое) поделен на 100 частей, и мы можем делить эти 100 фрагментов на любое количество долей. Все, что получится, будет сотыми частями целого. ¹/₄ = 100: 4 = 25 сотых, то есть ²⁵/₁₀₀ или 0,25. Деление совершается делением числителя на знаменатель: 1:4 = 0,25.

 Третья серия вкладышей: равные по площади фигуры.

Этот материал позволяет вычислять площади разных фигур и дает предварительное представление о некоторых геометрических теоремах, которые обычно не изучаются в начальной школе. Считается, что это недоступно пониманию маленьких детей.

Треугольник и прямоугольник равны по площади, если одна сторона прямоугольника равна основанию треугольника, а другая сторона прямоугольника равна половине высоты треугольника.

На широкой прямоугольной рамке есть два белых пространства (две выемки): равные по площади треугольник и прямоугольник.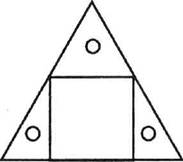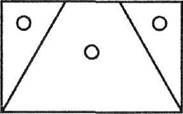

Вкладыши составлены так, что могут заполнить и прямоугольное, и треугольное пространство. Это треугольник, состоящий из трех частей.

Параллельная линия делит высоту треугольника пополам, вертикальная делит верхнюю часть на два равных треугольника. Можно наложить эти маленькие верхние треугольнички друг на друга и убедиться, что они равны.

Работа с бусинами и числовым квадратом научила детей находить площадь квадрата, умножая одну сторону на другую. Площадь прямоугольника также равна произведению смежных сторон. Работая с вкладышами, ребенок видит, что треугольник превращается в прямоугольник. Значит, их площади равны. Следовательно, площадь треугольника равна произведению его основания на половину высоты.

Равны площади ромба и прямоугольника, если одна сторона прямоугольника равна стороне ромба, а вторая — высоте ромба.

Вкладыши состоят из ромба, разделенного диагональю на два равных треугольника, и прямоугольника, разделенного на три треугольника таким образом, что они могут заполнить и ромбовидное пространство рамки, и прямоугольное. В комплект входят и целые фигуры ромба и прямоугольника. Если их наложить друг на друга, можно убедиться, что высоты равны. Равенство площадей фигур доказывается перемещением трех частей прямоугольника в ромбовидное пространство и обратно в прямоугольное. Отсюда следует очевидный вывод, что площадь ромба равна произведению стороны на высоту. (Площадь прямоугольника ребенок уже умеет вычислять.)

Равны площади трапеции и прямоугольника, если одна из сторон прямоугольника равна сумме двух оснований трапеции, а вторая — равна половине высоты трапеции. Ребенок может обнаружить и второй вариант равенства площади трапеции и прямоугольника. Если одна сторона прямоугольника равна высоте трапеции, а вторая — полусумме двух оснований.

Для этого достаточно разделить длинный прямоугольник пополам и положить одну часть над другой, образовав прямоугольник короче и шире первого. Большая прямоугольная рамка содержит три углублунных пространства: два трапецевидных (одинаковых) и одно прямоугольное, равное по площади, чья длина равна сумме двух оснований, а высота — половине высоты трапеции. Вкладыш в одну трапецию состоит из двух частей. Трапеция как бы разрезали по горизонтали на уровне половины высоты. Наложив обе части друг на друга, можно убедиться, что высоты равны. Вторая трапеция разделена на 4 части, которыми можно заполнить и прямоугольное пространство.

Равенство площадей двух фигур очевидно, а значит, можно понять, как вычислить площадь трапеции (умея вычислять площадь прямо-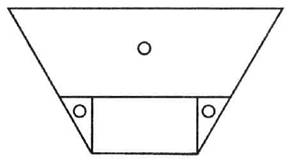

угольника): произведение суммы двух оснований на половину высоты, или произведение полусуммы оснований на высоту. Ученики, измерив стороны фигур, могут произвести арифметические вычисления.

Равны площади правильного многоугольника и прямоугольника, если одна сторона прямоугольника равна периметру многоугольника, а вторая — половине апофемы.

Есть две отдельные рамки с углублениями в форме многоугольника. Один вкладыш представляет собой целый многоугольник, второй — многоугольник, разделенный на треугольники. К примеру, возьмем десятиугольник, значит, и треугольников будет 10. На отдельной рамке — прямоугольное углубление, которое можно заполнить треугольниками, разделенными горизонтальным разрезом на две половинки на уровне половины высоты (два треугольника должны быть еще разделены пополам вертикальным разрезом).

В геометрическом альбоме рисуем таблицу, демонстрирующую равенство площадей десятиугольника и прямоугольника. Рисуем отдельно развертку десятиугольника — 10 треугольников в ряд, горизонтальной пунктирной линией обозначаем уровень половины высоты треугольника. Рядом (параллельно) нужных размеров прямоугольник, а рядом прямоугольник, в который «врисованы» треугольники.

Из 10 треугольников-вкладышей можно без рамки сложить еще один прямоугольник (один треугольник при этом делится еще на два равных треугольничка вертикальным разрезом) и убедиться, что площадь многоугольника равна площади прямоугольника, одна сторона которого равна целой апофеме многоугольника, а другая — половине периметра. Становится понятно, что площадь правильного многоугольника равна произведению периметра на половину апофемы, или произведению апофемы на половину периметра.

1. Умея вычислять площадь треугольника, ребенок понимает, что все треугольники с одинаковыми основаниями и высотами равны по площади.

Для осознания этой теоремы мы приготовили специальный материал. Равные по площади ромб и прямоугольник. Каждая фигура разделена на два равных треугольника. Эти треугольники разные по форме, но равные по площади. Равенство их оснований и высот можно проверить и измерениями, и наложением фигур. Равенство площади треугольников очевидно, ибо эти треугольники представляют половины равных по площади фигур. (Равенство ромба и прямоугольника уже было доказано и проверено.)

2. Теорема Пифагора. Квадрат гипотенузы прямоугольного тре

угольника равен сумме квадратов двух катетов.

1) два катета равны между собой;

2) катеты относятся друг к другу как 3:4;

3) общий случай.

1) Два катета равны между собой. На рамке — прямоугольный равнобедренный треугольник. Каждая сторона треугольника одновременно является стороной квадрата. Квадраты катетов по диагонали поделены на два треугольника каждый. Квадрат гипотенузы двумя диагоналями разделен на 4 треугольника. Получается всего 8 треугольников совершенно одинаковых. Треугольники катетов могут быть уложены в квадрат гипотенузы и наоборот. Эти перемещения увлекают детей, особенно если учесть, что треугольники квадратов катетов выкрашены в один цвет, а 4 треугольника квадрата гипотенузы — в другой.

2) Катеты относятся друг к другу как 3: 4. Квадраты сторон треугольника делятся не на треугольники, как в первом материале, а на квадраты. Квадрат первого (меньшего) катета поделен на 9 квадратиков (3 в квадрате) одного цвета, квадрат второго катета разделен на 16 (4 в квадрате) квадратиков другого цвета, квадрат гипотенузы разделен на 25 (5 в квадрате) квадратиков третьего цвета. Игра с перемещениями очевидна. Квадраты двух катетов могут быть заполнены квадратиками из квадрата гипотенузы. А квадрат гипотенузы можно красиво выложить разноцветными квадратиками квадратов катетов.

3) Общий случай. Рамка вкладышей — это большой прямоугольник размером 44x24 см. Ее можно сравнить с шахматной доской, где перемещаемые фигурки создают самые разные комбинации.

Понимание теоремы строится на нескольких уже освоенных принципах. Во-первых, два четырехугольника с одинаковым основанием и высотой равны по площади. Во-вторых, две фигуры, равные по площади третьей, равны по площади между собой.

Квадрат гипотенузы в данном материале разделен на два прямоугольника. Разделительная линия начинается в той точке, куда падает высота треугольника, опущенная из противолежащего угла. Кроме того, среди вкладышей есть два ромбоида. У одного сторона равна стороне квадрата большего катета, у второго — стороне квадрата меньшего катета. И у каждого ромбоида вторая сторона равна стороне квадрата гипотенузы. Меньшая высота этих ромбоидов равна высоте прямоугольников (части квадрата гипотенузы), большая высота равна сторонам квадратов катетов. Ребенку не обязательно заранее знать все эти соотношения величин. Он видит фигуры-вкладыши, красные и желтые, и просто перекладывает их, размещая в ячейках рамки. Кроме ячеек треугольной и квадратной формы (3 квадрата у каждой стороны треугольника) на той же рамке есть прямоугольные углубления для понимания соотношения высот и сторон ромбоидов. Материальное размещение подвижных фигурок на белом пространстве дает ученику возможность понять суть теоремы. Это не абстрактное заучивание соотношения величин, а простое и очень интересное упражнение.

Тот же материал может быть использован и для других целей.

Возьмем вкладыши для изучения теоремы Пифагора, уже размещенные на рамке. Сначала снимем два прямоугольника (части квадрата гипотенузы) и положим их в прямоугольные углубления. Опустив треугольник, положим на пустые места ромбоиды. Сначала это пространство было заполнено треугольником и двумя прямоугольниками, теперь — треугольником и двумя ромбоидами. Итак, сумма двух прямоугольников равна сумме двух ромбоидов. Теперь мы можем продемонстрировать равенство площадей ромбоидов и квадратов катетов. Опять уложим все вкладыши в исходном порядке и обратим внимание на пространство, занятое треугольником и квадратом большего катета. Для этого снимем уложенные в него фигуры и заполним другими:

– снова треугольником и большим квадратом;

– треугольником и большим ромбоидом.

То же можно проделать с пространством, заполненным треугольником и квадратом меньшего катета. Только придется взять меньший ромбоид.

Можно убедиться в равенстве площади ромбоидов и соответствующих прямоугольников и квадратов. Для этого фигуры помещаем в боковые прямоугольники на рамке и убеждаемся в равенстве высот фигур. Равенство оснований проверяется их наложением друг на друга. Следовательно, фигуры равны по площади.

Наша геометрическая система включает в себя и другие материалы, но менее значимые.

Четвертая серия вкладышей: деление треугольника.

Четыре одинаковые рамки с одинаковыми углублениями треугольной формы (равносторонними, сторона 10 см) и треугольниками-вкладышами. Один треугольник — цельная фигура. Второй — 2 равных разносторонних прямоугольных треугольника. Они получились разделением равностороннего треугольника линией высоты. Третий треугольник состоит из трех тупоугольных равнобедренных треугольников, получившихся от деления углов биссектриссами. Наконец, четвертый разделен на 4 равносторонних треугольника, подобных большому треугольнику.

Ребенок может измерять углы, научиться отличать прямой угол от острого и тупого. Измеряя все углы треугольника, ученик узнает, что сумма углов треугольника всегда составляет 180°, то есть два прямых угла. Он может заметить, что углы равностороннего треугольника равны (60°). В равнобедренном треугольнике два угла, прилегающие к основанию, равны между собой. В разностороннем треугольнике все углы разные. В прямоугольном треугольнике сумма двух острых углов равна 90°, то есть прямому углу. Ученик может самостоятельно вывести определение: треугольники подобны, если их соответствующие углы равны.

Материал для изучения вписанных и описанных фигур

Этот материал напоминает уже описанный. На белом фоне можно располагать фигуры вписанные или описанные. К примеру, в центре большого равностороннего треугольника расположим маленький красный равносторонний треугольник (четвертая часть большого). Каждая вершина маленького треугольника касается средней точки каждой стороны большого треугольника.

Еще есть квадраты разной величины. В рамках для них сделаны соответствующие белые углубления. Квадрат со стороной 7 см может быть уложен в центр квадрата со стороной 10 см так, чтобы каждая вершина касалась середины каждой стороны. То же можно сделать с квадратами со стороной 7 и 5 см, 5 и 3,5 см.

Есть еще и круги разного диаметра. Их можно накладывать друг на друга, накладывать на них треугольники. Круг с диаметром 10 см вписывается в квадрат со стороной 10 см.

Все эти соотношения делают разноцветные вкладыши чрезвычайно удобными для рисования различных красивых сочетаний.

В этот материал мы включили и звезды, которые обычно служат для декоративного рисования, и цветы, образованные пересечением кругов и полукружий.

Беглое изложение перспектив развития геометрических знаний

Приходит момент, когда дети с удовольствием и знанием дела вычисляют площади правильных геометрических фигур. К этому их подготовили упражнения с бусинами, с квадратами и кубами чисел. Теперь им нетрудно научиться высчитывать объем геометрического тела. Тем более полезно после упражнений с кубом чисел (при помощи бусин) узнать, что произведение площади основания на высоту равно объему призмы.

Материал состоит из трех геометрических тел: призмы, пирамиды (ее основание и высота равны основанию и высоте призмы) и призмы, чье основание равно основанию пирамиды, а высота втрое меньше. Фигуры полые. Призмы закрыты крышкой и являются, по существу, коробочками. У пирамиды нет крышки снизу, с ее помощью можно набирать и перекладывать разные субстанции. Мы наполняем тела разными субстанциями (песок или зерна проса) так, чтобы заполнить их целиком и чтобы содержимое оставалось всегда в том же количестве. Это нелегко. Часто вещество насыпают не доверху, получается меньший объем, чем присущ телу на самом деле. Нужно научиться заполнять пустоту так же, как нужно научиться укладывать вещи максимально компактно. Покачивать тело, чтобы утрясти содержимое, разглаживать и приминать поверхность — детям это очень нравится.

Тело можно наполнить и жидкостью. В этом случае придется научиться переливать жидкость, не теряя первоначального объема, не проливая ни капли.

Это техническая подготовка к измерительной процедуре. Ученики узнают, что объем пирамиды равен объему маленькой призмы, то есть трети объема большой призмы. Следовательно, объем пирамиды равен произведению площади основания на треть высоты.

Наполнив глиной маленькую призму, мы получим достаточный объем, чтобы заполнить пирамиду. Из этой глины можно сделать два тела, равные по объему, по форме совпадающие с телами нашего материала. Пять равных частей глины, достаточных, чтобы заполнить маленькую призму, станут материалом для пяти тел.

Из этой идеи вытекают все остальные действия: объяснения почти не нужны. Часто исследования возникают как следствие детских вопросов.

– Как найти площадь круга?

– Как найти объем цилиндра?

– А конуса?

Вычисление площади поверхности тела — прекрасная задача для ребенка. Иногда ребенок спонтанно находит ответ. Материал для этого такой: деревянные геометрические тела, у которых основное измерение — 10 см:

– четырехугольный параллелепипед (10, 10, 20 см);

– четырехугольный параллелепипед, равный трети первого;

– четырехугольная пирамида (10,10, 20 см);

– треугольная призма (10, 20 см);

– треугольная призма, равная трети предыдущей;

– пирамида (10, 20 см);

– цилиндр (диаметр 10 см, высота 20 см);

– цилиндр, втрое меньше предыдущего;

– конус (диаметр 10 см, высота 20 см);

– сфера (ось 10 см);

– овал (большая ось 10 см);

– эллипсоид (большая ось 10 см).

А также тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр. Эти тела раскрашены в разные цвета.

Сила чисел

Материал: два равных куба с ребром 2 см, призма вдвое больше куба, призма вдвое больше предыдущей, 7 кубов с ребром 4 см. Два кубика, рядом стоящие, — 2. Два кубика и призма вдвое больше куба — 2². Все то же и самая большая призма -2³. Два кубика с гранью 4 см — 2⁴

Добавить к ним еще 2 кубика — 2⁵.

Добавить к ним еще 4 кубика — 2⁶.

Итак, 2³, 2⁶ — фигуры располагаются в форме куба.

2², 2⁵ — фигуры располагаются в форме квадрата.

2, 2⁴ — фигуры располагаются в одну линию.

 (а + b)³ = a³ + b³ + За²b + 3b²a

Материал: куб (ребро 6 см), куб (ребро 4 см), 3 призмы с квадратным основанием (сторона 4 см, высота 6 см), 3 призмы с квадратным основанием (сторона 6 см, высота 4 см).

Вес и размер

В распоряжении детей всегда есть много предметов для взвешивания и измерения. Например, еще в Доме ребенка ученики пользовались счетными штангами для измерения длины. Эта система имела свой метр и более мелкие деления, дециметры. Сейчас в распоряжении младших школьников десятиметровая лента, которой можно измерить пол, а значит, вычислить его площадь. Есть метровые измерители в разных формах (линейка, металлическая лента, швейный сантиметр и штанга торговца). Дети измеряют всем подряд и все подряд, с удовольствием высчитывают площади нарисованных геометрических фигур или вкладышей.

Устанавливается связь между длиной, площадью и объемом, соединяются в систему три измерения: длина, высота и ширина. Более глубоко изучаются хорошо знакомые материалы, вроде розовой башни.

Дети учатся пользоваться различными научными приборами: термометром, весами, осваивают систему мер и весов. Наполним водой кубический дециметр (полый куб со стороной 10 см) — получим литр. Теперь можно измерить объем бутылки и маленького пузырька.

Ученики измеряют температуру воды в различных состояниях. Здесь не стоит останавливаться на частностях. Большая часть предложенных нами задач придумана детьми. Вот ясное свидетельство легкости достижения внешних результатов при готовности внутреннего состояния.